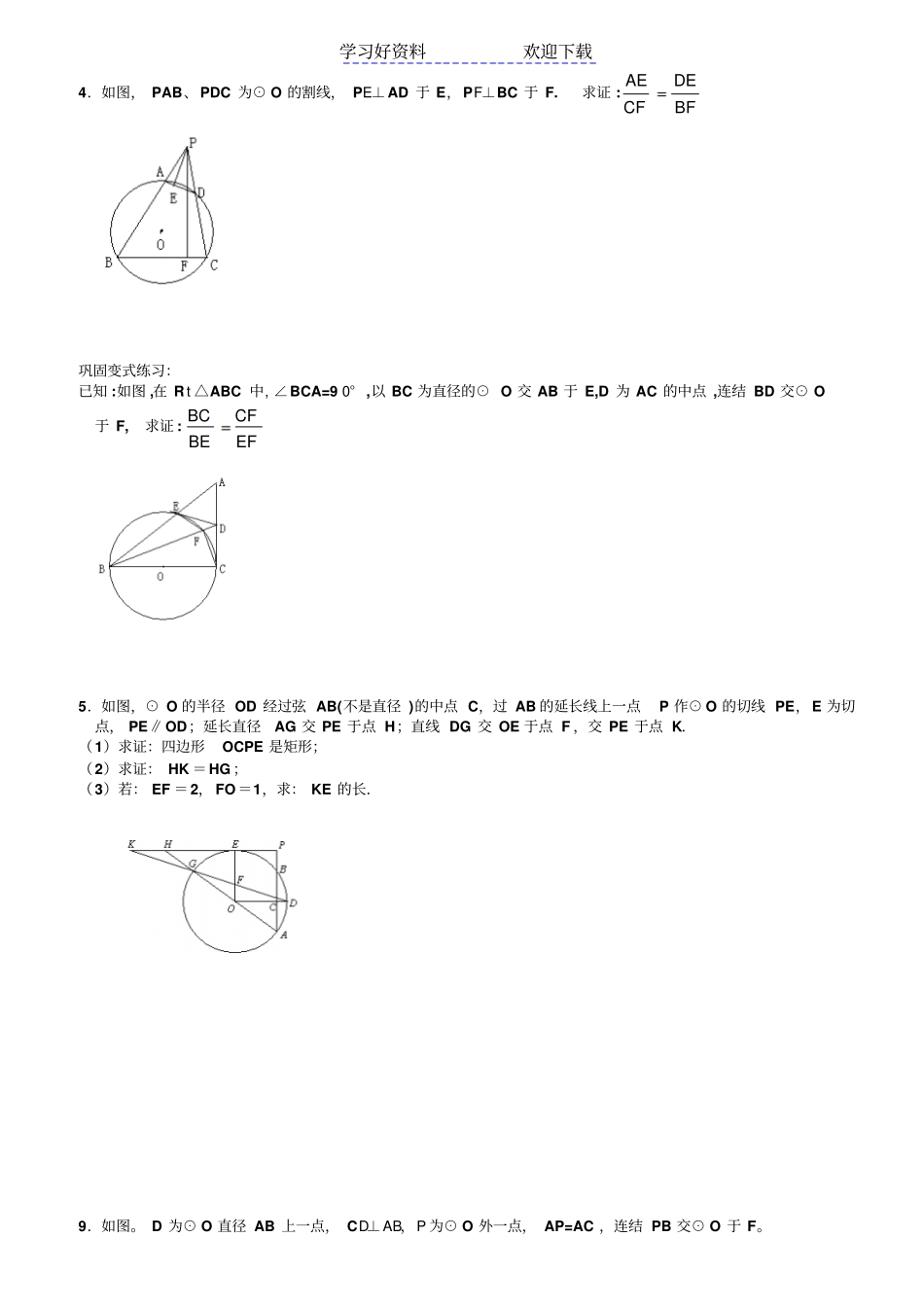
学习好资料欢迎下载圆压轴题思路分析姓名一.指点迷津:1.计算:勾股定理、相似、三角形函数(特殊角的三角形函数值顺、逆向运用)、方程思想、字母化。2.圆知识:垂径定理、切线判定性质、圆周角与圆心角关系、圆内接四边形、同圆半径相等的转化、五量定理。3.圆的角的转移:圆外角、圆内角向圆上角转移;转移工具:平行线性质、相似(特别注意射影定理模型图转移)、圆内接四边形性质、关注公弧借圆周角定理转移、关注同弧所对的圆心角与圆周角4.注重相关知识的运用:等腰三角形性质、角平分线、垂直平分线、全等三角形5.热点考查预测:相似的“SAS”定理( S 量的计算思路) 、含两个特殊角的三角函数计算模型思路、从数据中寻找隐含关系------- 特殊角和假射影定理相似模型6.技巧:善于从图中寻找几何基本模型图二.基本训练:1.如图,⊙ O 是△ ABC 的外接圆, BC 是⊙ O 的直径, D 是劣弧 AC 的中点, BD 交 AC 于点 E. ⑴ 求证:2ADDE DB⑵若: BC52, CD52,求:DE 的长2.如图,在Rt△ABC 中,∠ C=90° ,以 BC 边为直径的⊙ O 交 AB 于 D,连接 OD 并延长交CA 的延长线于点 E,过点 D 作 DF⊥OE 交 EC 于点 F. (1)求证: AF=CF ;(2)若 ED=2 ,sin∠E=53 ,求:AD 的长 . 3.如图 ,AB 是△ ABC 的外接圆⊙ O 的直径 ,D 是⊙ O 上一点 ,DE⊥AB 于点 E,且 DE 的延长线分别交AC 。⊙O 和 BC 的延长线于点F、M 、G. (1)求证 :AE·BE=EF ·EG (2)连接 BD,若 BD⊥BC,若 EF=MF=2, 求: AE 和 MG 的长 . 学习好资料欢迎下载4.如图, PAB、PDC 为⊙ O 的割线, PE⊥AD 于 E,PF⊥BC 于 F. 求证 :BFDECFAE巩固变式练习:已知 :如图 ,在 Rt △ABC 中, ∠BCA=9 0° ,以 BC 为直径的⊙ O 交 AB 于 E,D 为 AC 的中点 ,连结 BD 交⊙ O 于 F, 求证 :EFCFBEBC5.如图,⊙ O 的半径 OD 经过弦 AB(不是直径 )的中点 C,过 AB 的延长线上一点P 作⊙ O 的切线 PE,E 为切点, PE∥OD;延长直径AG 交 PE 于点 H;直线 DG 交 OE 于点 F ,交 PE 于点 K.(1)求证:四边形OCPE 是矩形;(2)求证: HK =HG ;(3)若: EF =2, FO=1,求: KE 的长.9.如图。 D 为⊙ O 直径 AB 上一点, CD⊥AB,P 为⊙ O 外一点, AP=AC ,连结 PB 交⊙ O 于 F。...