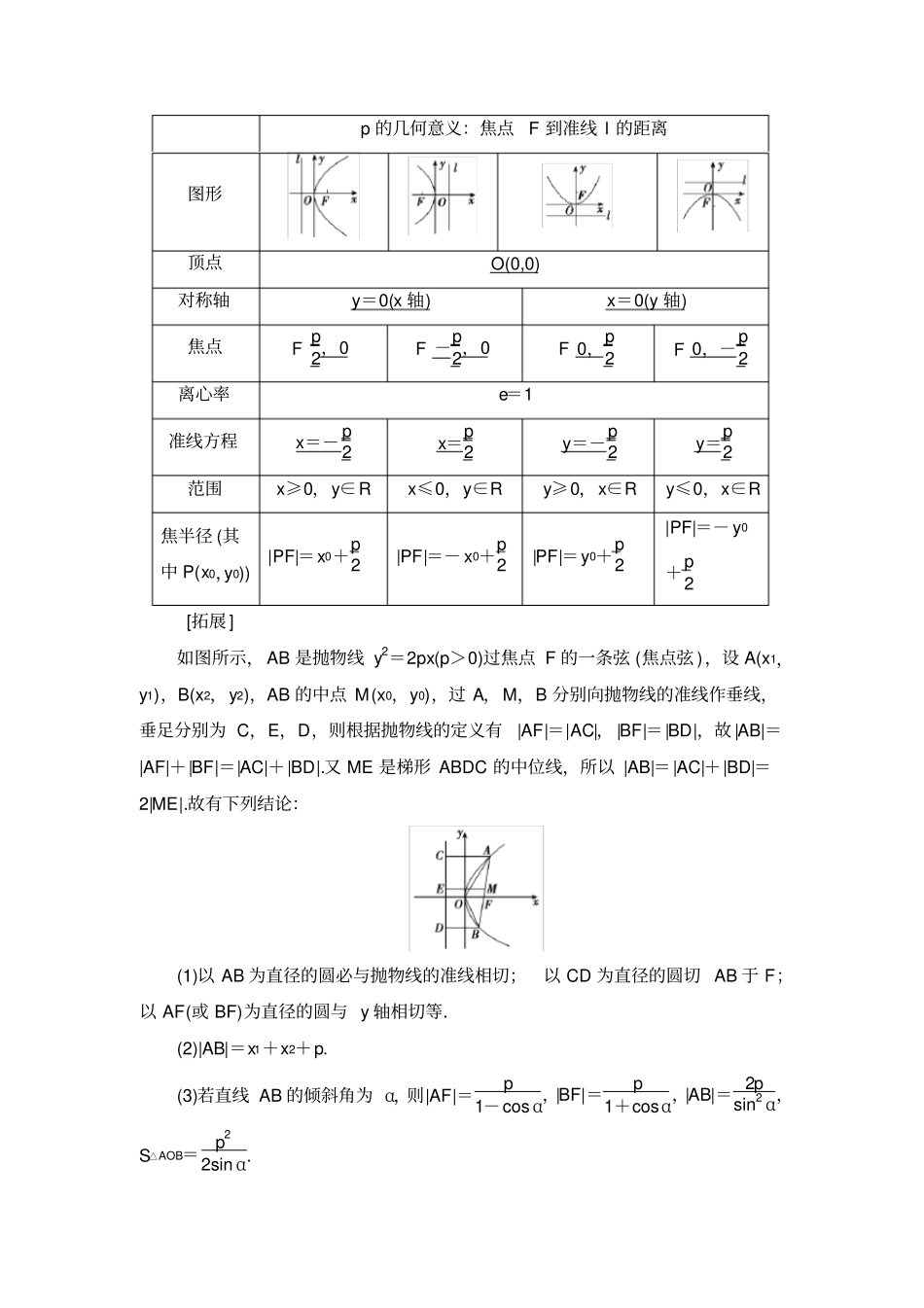
圆锥曲线的方程和性质知识点一、椭圆知识点 1椭圆的定义(1)平面内与两个定点F1,F2的距离之和等于常数2a(大于 |F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.(2)椭圆定义的数学表达式为|PF1|+|PF2|=2a(2a>|F1F2|),即对于定点F1,F2,椭圆上的点 P 满足此关系式,反之亦然.思考: 集合 P={ M||MF 1|+|MF 2|=2a} ,|F1F2|=2c,其中 a,c 为常数且 a>0,c>0.M 点轨迹为椭圆吗?提示: ①当 2a>|F1F2|时, M 点的轨迹为椭圆;②当 2a=|F1F2|时, M 点的轨迹为线段 F1F2;③当 2a<|F1F2|时, M 点的轨迹不存在.知识点 2椭圆的标准方程及几何性质焦点在 x 轴上焦点在 y 轴上标准方程x2a2+y2b2=1(a>b>0)y2a2+ x2b2=1(a>b>0) 一般方程Ax2+By2=1(A>0,B>0,A≠B) 图形焦点坐标F1(-c,0),F2(c,0)F1(0,- c),F2(0,c) 顶点坐标A1(-a,0),A2(a,0),B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),B1(-b,0),B2(b,0) 长轴长轴 A1A2=2a,a 是长半轴的长短轴短轴 B1B2=2b,b 是短半轴的长焦距焦距 F1F2=2c,c 是半焦距范围|x|≤a,|y|≤b |x|≤b,|y|≤a离心率e= ca=1-b2a2(0<e<1) e 越接近 1,椭圆越扁; e 越接近 0,椭圆越圆[拓展 ]1.如图,过椭圆的一个焦点且与长轴垂直的弦|AB|=2b2a ,称为通径.2.如图, P 为椭圆上的点, F1,F2 为椭圆的两个焦点,且∠F1PF2=θ,则△F1PF2 的面积为 b2·tan θ2. 3.椭圆 x2a2+y2b2=1 与x2a2+y2b2=k(其中 a>b>0,k>0)有相同的离心率.4.a+c 与 a-c 分别为椭圆上的点到焦点距离的最大值和最小值.5.设 P,A,B 是椭圆上不同的三点,其中A,B 关于原点对称,则直线PA与 PB 的斜率之积为定值- b2a2. 二、抛物线知识点 1抛物线的定义平面内到一定点 F 和定直线 l(F?l)距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l 叫做抛物线的准线.思考: 在抛物线的定义中,若F∈l 时,动点的轨迹怎样?提示:当定点在定直线上时, 轨迹为过定点 F 且与定直线 l 垂直的一条直线.知识点 2抛物线的标准方程与几何性质标准方程y2=2px(p>0) y2=- 2px(p>0) x2=2py(p>0) x2=- 2py(p>0) p 的几何意义:焦点F 到准线 l 的距离图形顶点O(0,0) 对称轴y=0(x 轴)x=0(y 轴) 焦点F p2,0F -p2,0F 0,p2F 0...