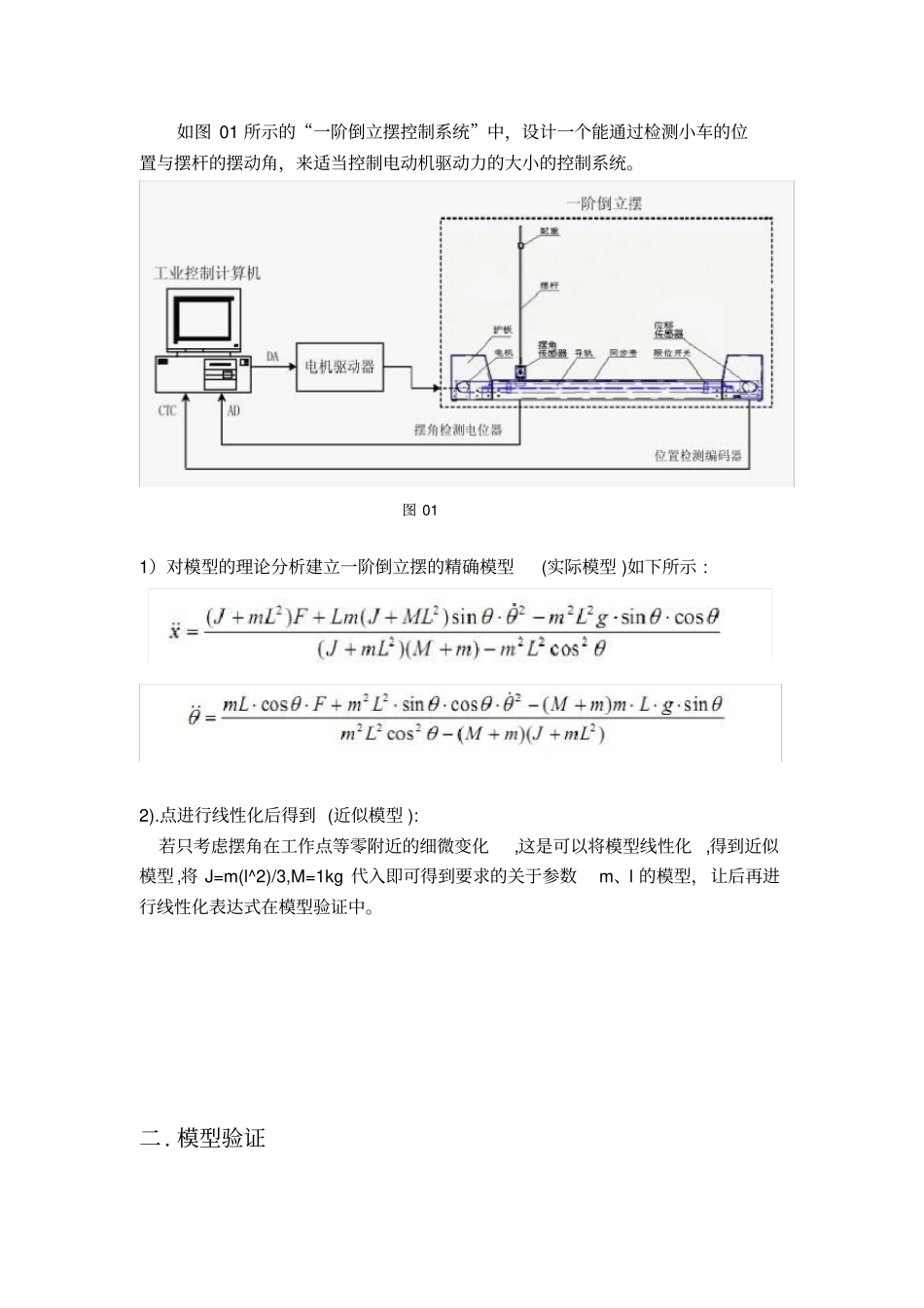
本科生课程设计题目: 基于双闭环PID 控制的一阶倒立摆控制系统设计姓名:学号:系别:电气工程系专业:电气工程与自动化年级: 07级指导教师: 2010 年4 月28 日目录1、系统模型的建立 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3. 2、模型验证 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.⋯⋯⋯ . 4.3、设计的内外环的 PID 控制器 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10. 4、SIMULIN仿真⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯... 13. 5、检测系统的鲁棒性 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16. 6、遇到问题 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯19. 7、心得体会 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..20. 8、结论⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯...⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 21. 9、参考文献 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..22.一. 系统模型的建立如图 01 所示的“一阶倒立摆控制系统”中,设计一个能通过检测小车的位置与摆杆的摆动角,来适当控制电动机驱动力的大小的控制系统。图 01 1)对模型的理论分析建立一阶倒立摆的精确模型(实际模型 )如下所示 : 2).点进行线性化后得到 (近似模型 ): 若只考虑摆角在工作点等零附近的细微变化,这是可以将模型线性化 ,得到近似模型 ,将 J=m(l^2)/3,M=1kg 代入即可得到要求的关于参数m、l 的模型,让后再进行线性化表达式在模型验证中。二. 模型验证1)子系统的建立实际模型图 1 Fcn:(((4*m*(l^2))/3)*u[1]+l*m*((4*m*(l^2))/3)*sin(u[3])*(u[2]^2)-10*(m^2)*(l^2)*sin(u[3])*cos(u[3]))/(((4*m*(l^2))/3)*(1+m)-(m^2)*(l^2)*power(cos(u[3]),2)) Fcn1:(m*l*cos(u[3])*u[1]+(m^2)*(l^2)*sin(u[3])*cos(u[3])*(u[2]^2)-10*(1+m)*m*l*sin(u[3]))/((m^2)*(l^2)*power(cos(u[3]),2)-(1+m)*(4*m*(l^2))/3) 线性模型图 2Fcn2:(30*(1+m*u[2]-3*u[1])/(l*(4+m) Fcn3:(5*u[1]-30*m*u[2])/(4+m) 做完以上之后点击鼠标左键不放对图形进行选定,接着右击 creat subsystem如下图所示 :图 32)模型的封装:倒立摆的振子质量m和倒摆长度L 作为子系统的参数:图 4 双击函数模块 : 图 5欲改变其中的任一个参数只要点击其中二者之一的函数方块就行,在其中的 m,l 改就行了。有两种实现的方法:一种是利用示波器观察如下图所示,另一种是采用绘图程序实现。1)示波器实现如图6:图 6 示波器显示结果如图7 所示图 7 2)用程序实现...