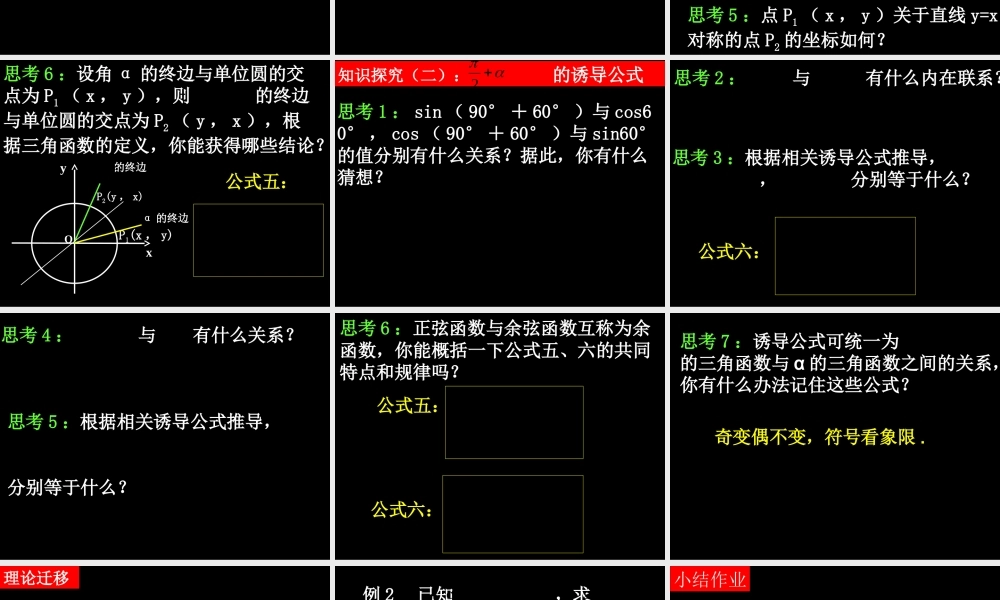
1.3 三角函数的诱导公式第二课时 问题提出1. 诱导公式一、二、三、四分别反映了2kπ+α ( k∈Z )、 π + α 、- α 、 π - α 与 α 的三角函数之间的关系,这四组公式的共同特点是什么?cosx cosx 函数同名,象限定号 . 2. 对形如 π - α 、 π + α 的角的三角函数可以转化为 α 角的三角函数,对形如 、 的角的三角函数与α 角的三角函数,是否也存在着某种关系,需要我们作进一步的探究 . 22pa+ 思考 1 : sin ( 90° - 60° )与 sin60°的值相等吗?相反吗?思考 2 : sin ( 90° - 60°) 与 cos60° ,cos ( 90° - 60° )与 sin60° 的值分别有什么关系?据此,你有什么猜想? 2cos)2(sin知识探究(一): 的诱导公式 2cos)2(sincos()sin2paa-= cos)2(sin思考 3 :如果 α 为锐角,你有什么办法证明 , ?cos()sin2paa-=αabc2pa-sin()cos2bcpaa-==cos()sin2acpaa-== 思考 5 :点 P1 ( x , y )关于直线 y=x对称的点 P2 的坐标如何?思考 4 :若 α 为一个任意给定的角,那么 的终边与角 α 的终边有什么对称关系? 2α 的终边Oxy的终边 2 思考 6 :设角 α 的终边与单位圆的交点为 P1 ( x , y ),则 的终边与单位圆的交点为 P2 ( y , x ),根据三角函数的定义,你能获得哪些结论? 2α 的终边P1(x , y)Oxy的终边 2P2(y , x) 公式五: sin)2cos(cos)2sin( 思考 1 : sin ( 90° + 60° )与 cos60° , cos ( 90° + 60° )与 sin60°的值分别有什么关系?据此,你有什么猜想?知识探究(二): 的诱导公式 2sin)2cos(cos)2sin( 思考 3 :根据相关诱导公式推导, , 分别等于什么?)2sin( )2cos( 公式六: sin)2cos(cos)2sin(思考 2 : 与 有什么内在联系? 2 2)2(2 思考 4 : 与 有什么关系?)2tan( tan思考 5 :根据相关诱导公式推导,分别等于什么?3sin(),2pa-3cos(),2pa-3sin(),2pa+)23cos( tan()tan12paa+= - 思考 6 :正弦函数与余弦函数互称为余函数,你能概括一下公式五、六的共同特点...