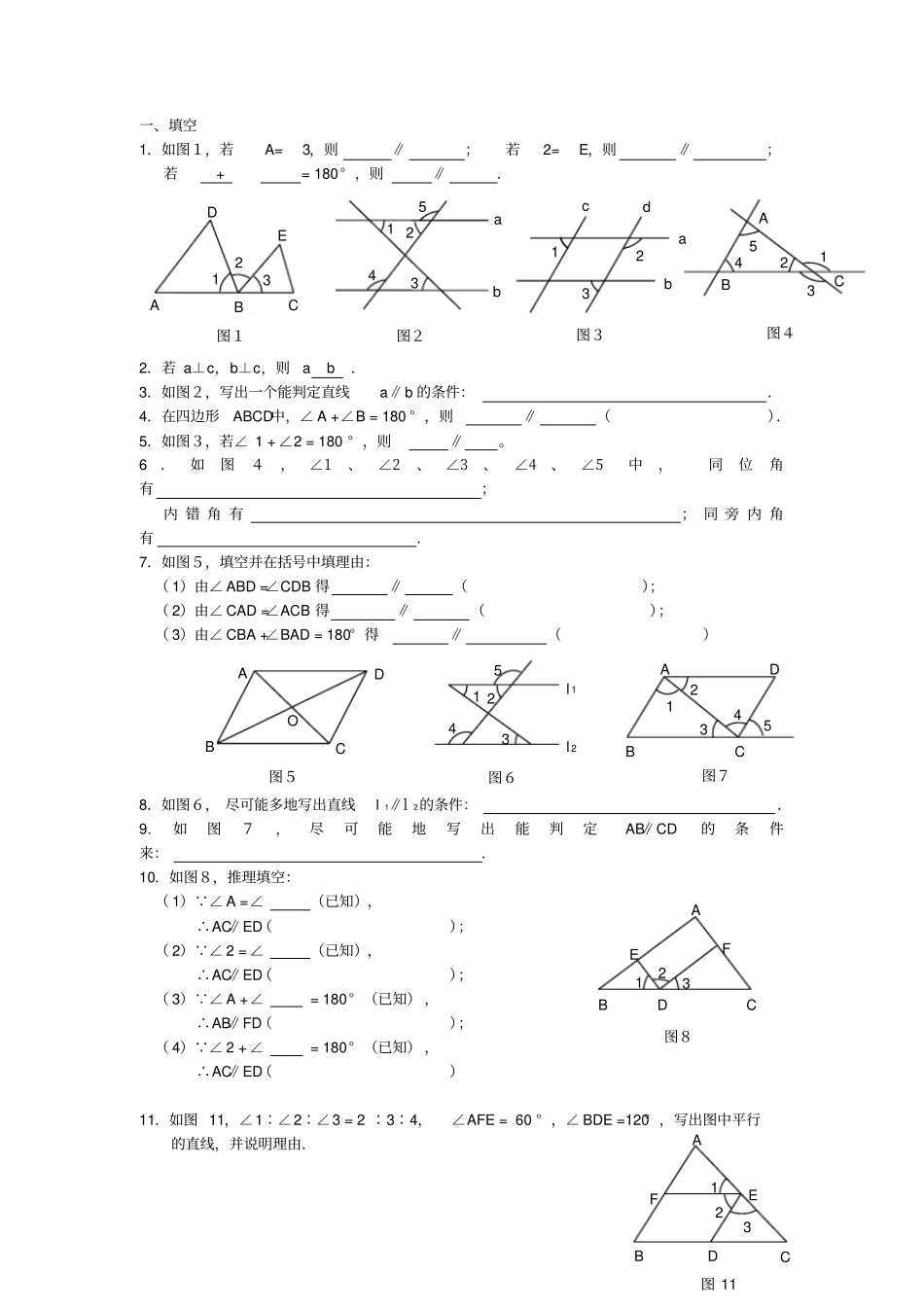
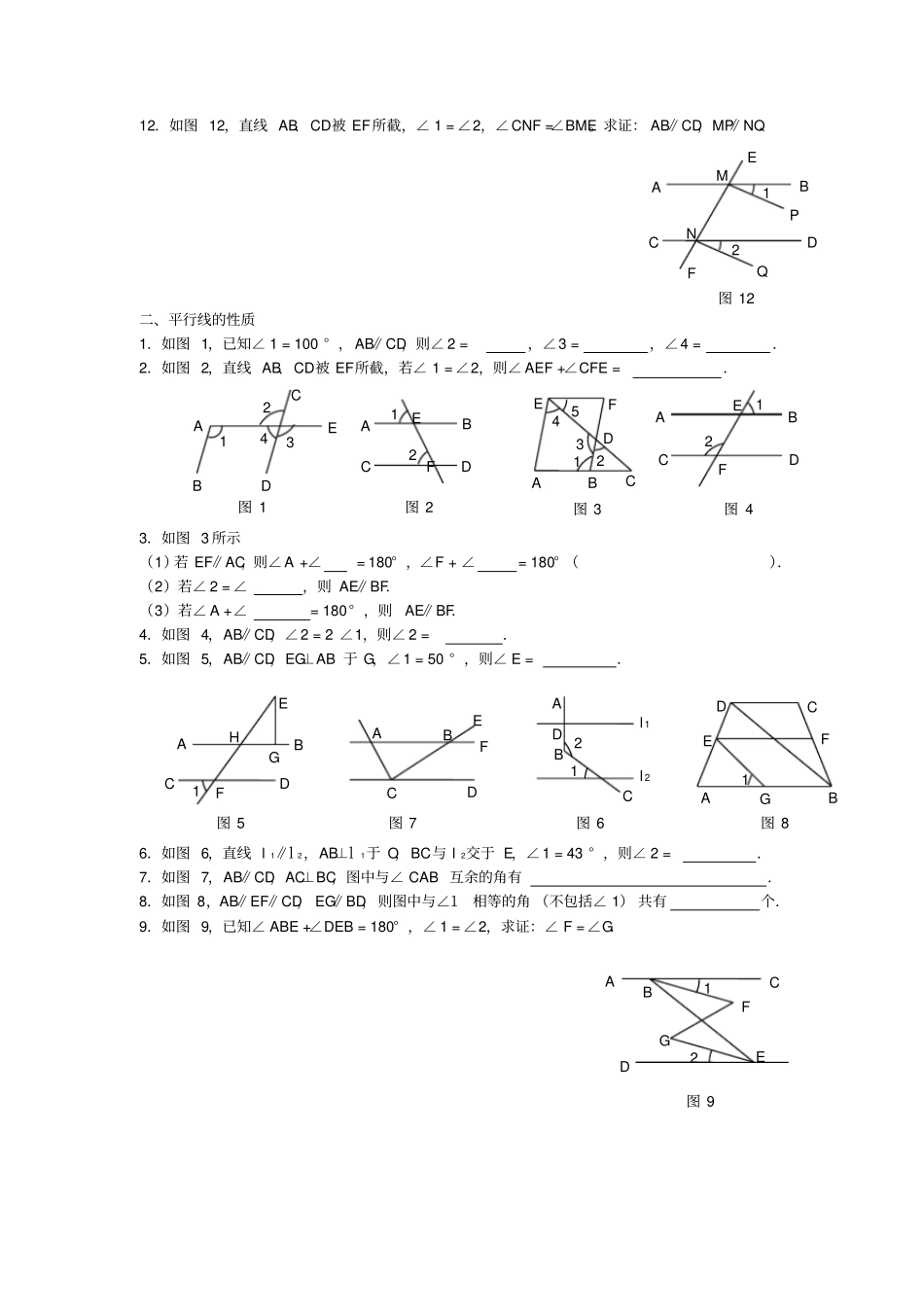
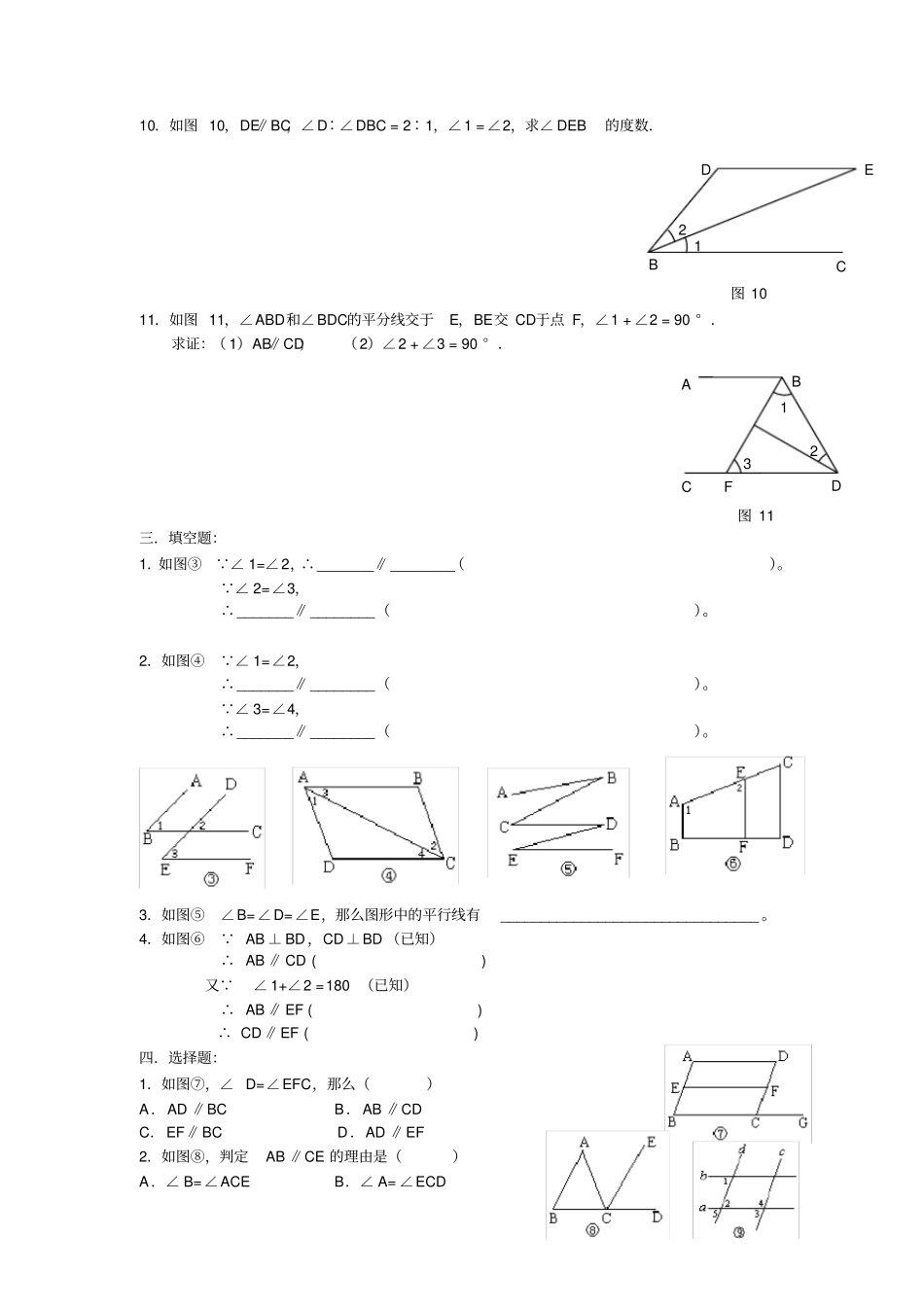
一、填空1.如图1,若A=3,则∥;若2=E,则∥;若 += 180° ,则∥.2.若 a⊥c,b⊥c,则a b.3.如图2,写出一个能判定直线a∥b 的条件:.4.在四边形ABCD中,∠ A +∠B = 180 ° ,则∥().5.如图3,若∠ 1 + ∠2 = 180 ° ,则∥。6.如图4,∠1、∠2、∠3、∠4、∠5中,同位角有;内 错 角 有; 同 旁 内 角有.7.如图5,填空并在括号中填理由:( 1)由∠ ABD =∠CDB 得∥();( 2)由∠ CAD =∠ACB 得∥();( 3)由∠ CBA +∠BAD = 180° 得∥()8.如图6, 尽可能多地写出直线l 1∥l 2的条件:.9.如图7,尽可能地写出能判定AB∥CD的条件来:.10.如图8,推理填空:( 1) ∠ A =∠(已知),∴AC∥ED();( 2) ∠ 2 = ∠(已知),∴AC∥ED();( 3) ∠ A +∠= 180° (已知) ,∴AB∥FD();( 4) ∠ 2 + ∠= 180° (已知) ,∴AC∥ED()11.如图 11,∠1∶∠2∶∠3 = 2 ∶3∶4,∠AFE = 60 ° ,∠ BDE =120° ,写出图中平行的直线,并说明理由.A C B 4 1 2 3 5 图4a b c d 1 2 3 图3A B C E D 1 2 3 图1图24 3 2 1 5 a b 1 2 3 A F C D B E 图8A D C B O 图5图65 1 2 4 3 l 1 l 2图75 4 3 2 1 A D C B 1 3 2 A E C D B F 图 11 12.如图 12,直线 AB、CD被 EF所截,∠ 1 = ∠2,∠CNF =∠BME。求证: AB∥CD,MP∥NQ.二、平行线的性质1.如图 1,已知∠ 1 = 100 ° ,AB∥CD,则∠ 2 =,∠3 =,∠4 =.2.如图 2,直线 AB、CD被 EF所截,若∠ 1 = ∠2,则∠ AEF +∠CFE =.3.如图 3 所示(1)若 EF∥AC,则∠A +∠= 180° ,∠F + ∠= 180° ().(2)若∠ 2 = ∠,则 AE∥BF.(3)若∠ A +∠= 180° ,则AE∥BF.4.如图 4,AB∥CD,∠2 = 2 ∠1,则∠ 2 =.5.如图 5,AB∥CD,EG⊥AB 于 G,∠1 = 50 ° ,则∠ E =.6.如图 6,直线 l 1∥l 2,AB⊥l1于 O,BC与 l 2交于 E,∠1 = 43 ° ,则∠ 2 =.7.如图 7,AB∥CD,AC⊥BC,图中与∠ CAB 互余的角有.8.如图 8,AB∥EF∥CD, EG∥BD,则图中与∠1相等的角 (不包括∠ 1) 共有个.9.如图 9,已知∠ ABE +∠DEB = 180° ,∠ 1 = ∠2,求证:∠ F =∠G.F 2 A B...