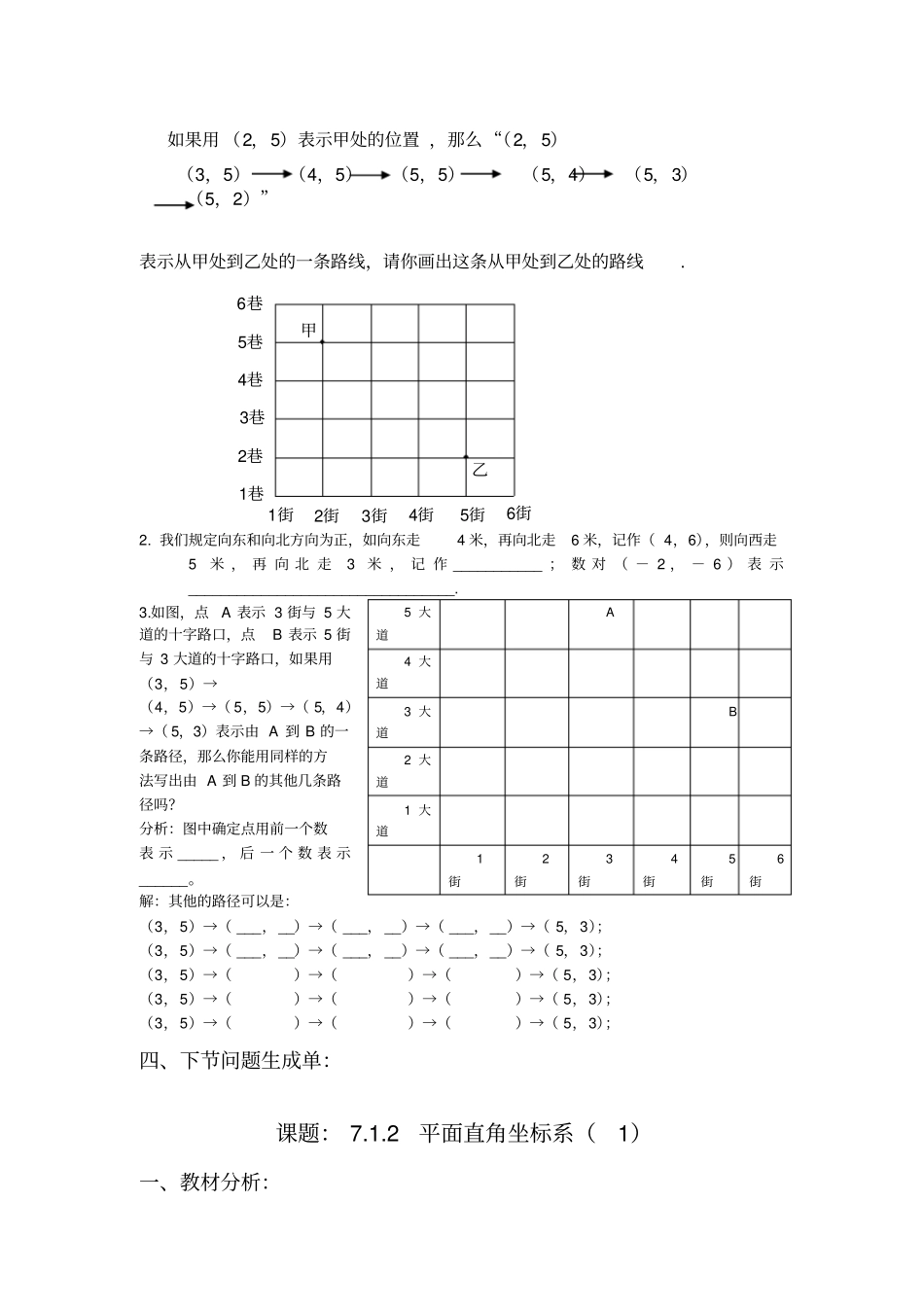
课题: 7.1.1有序数对一、教材分析:(一)学习目标:1. 经历用有序数对表示位置的过程,理解有序数对的意义. 2. 通过学习用有序数对表示位置,发展符号感及抽象思维能力. (二)学习重点和难点:1. 重点:用有序数对表示位置.2. 难点:对有序数对中的有序的理解.二、教学过程:1.任务导读单:阅读P64— 65 页回答下列问题:1.阅读本章彩页 ,说明类似于用“ _____________________”来确定同学的位置,从而建立平面直角坐标系. 2. 观 察 分 析P64页 彩 图 , 说 明 座 位 上 的 “7排9号 ” 的 含意:______________________ “7 排 9 号”的含意是 :____________________________.这说明在影剧院里 , 第个座位上必需用“ _____个数字”来确定座位的位置. 3. 在教室里你跟同学说明你的位置是: __________________________________ 2.互动探究 ,合作求解:A. 阅读 P65页中“思考”排数和列数先后顺序对位置是否有影响?__________, B. 按教 材 中 约 定 , 观 察 图7.1-1, 并 在 图 中标 注 位 置 ,(1,5),(2,4),(4,2),(3,3),(5,6)分别用 :A.B.C.D.E. 其中 (2,4) 和(4,2) 是表示___同的位置 , 这说明交换数对的两个数的顺序,数对所表示的座位就______了,也就说明数对的两个数是有序的C. 归纳:有序数对 : 我们把这种 ________的两个数 a 和 b 组成的数对 , 叫做有序数对, 记作 (a,b).其中这两个数各自表示____________.举例说明生活中利用有序数对表示位置的例如 :__________________________________________________ 3、达标训练:1. 如图,甲处表示2 街与 5 巷的十字路口,乙处表示5 街与 2 巷的十字路口 ,如果用 (2,5)表示甲处的位置 ,那么 “(2,5)(3,5)(4,5)(5,5)(5,4)(5,3)(5,2)”表示从甲处到乙处的一条路线,请你画出这条从甲处到乙处的路线. 2. 我们规定向东和向北方向为正,如向东走4 米,再向北走6 米,记作( 4,6),则向西走5米 , 再 向 北 走3米 , 记 作 ___________ ; 数 对 ( - 2 , - 6 ) 表 示_________________________________. 3.如图,点A 表示 3 街与 5 大道的十字路口,点B 表示 5 街与 3 大道的十字路口,如果用(3,5)→(4,5)→( 5,5)→( 5,4)→( 5,3)表示由 A 到 B 的一条路径,那么你能用同样的方法写出由 A 到 B 的其他...