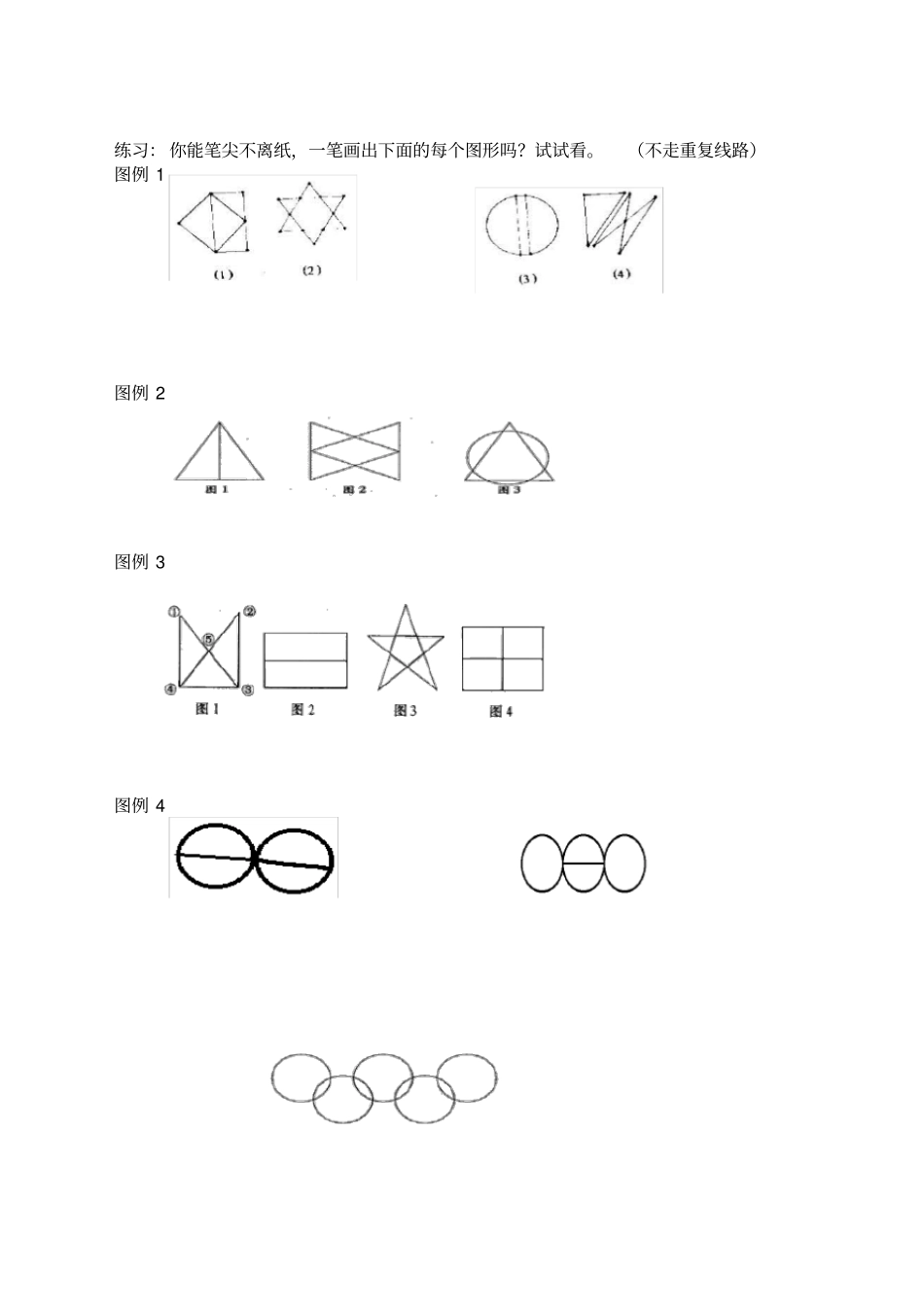
七年级上数学思维拓展训练第一章兴趣数学七桥问题(一笔画问题)18 世纪时,欧洲有一个风景秀丽的小城哥尼斯堡,那里有七座桥。如图1 所示:河中的小岛 A与河的左岸 B、右岸 C各有两座桥相连结,河中两支流间的陆地D与 A、B、C各有一座桥相连结。当时哥尼斯堡的居民中流传着一道难题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点?大家都试图找出问题的答案,但是谁也解决不了这个问题。七桥问题引起了著名数学家欧拉(1707— 1783)的关注。他把具体七桥布局化归为图所示的简单图形,于是,七桥问题就变成一个一笔画问题:怎样才能从A、B、C、D中的某一点出发,一笔画出这个简单图形(即笔不离开纸,而且a、b、c、d、e、f 、g 各条线只画一次不准重复),并且最后返回起点?欧拉经过研究得出的结论是:图是不能一笔画出的图形。这就是说,七桥问题是无解的。这个结论是如何产生呢?如果我们从某点出发,一笔画出了某个图形,到某一点终止,那么除起点和终点外,画笔每经过一个点一次,总有画进该点的一条线和画出该点的一条线,因此就有两条线与该点相连结。 如果画笔经过一个n 次,那么就有 2n 条线与该点相连结。 因此,这个图形中除起点与终点外的各点,都与偶数条线相连。如果起点和终点重合,那么这个点也与偶数条线相连;如果起点和终点是不同的两个点,那么这两个点部是与奇数条线相连的点。综上所述,一笔画出的图形中的各点或者都是与偶数条线相连的点,或者其中只有两个点与奇数条线相连。图 2 中的 A点与 5 条线相连结, B、C、D各点各与 3 条线相连结,图中有 4 个与奇数条线相连的点,所以不论是否要求起点与终点重合,都不能一笔画出这个图形。欧拉定理:如果一个图是连通的并且奇顶点的个数等于0 或 2,那么它可以一笔画出;否则它不可以一笔画出。一笔画:■⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。■⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点终点。■⒊其他情况的图都不能一笔画出。( 奇点数除以二便可算出此图需几笔画成。) 练习: 你能笔尖不离纸,一笔画出下面的每个图形吗?试试看。(不走重复线路)图例 1 图例 2 图例 3 图例 4 第二章 绝对值知识回顾:绝对值的意义(1) 代数意义 : 一个正数的绝对只是它本身,一个负数...