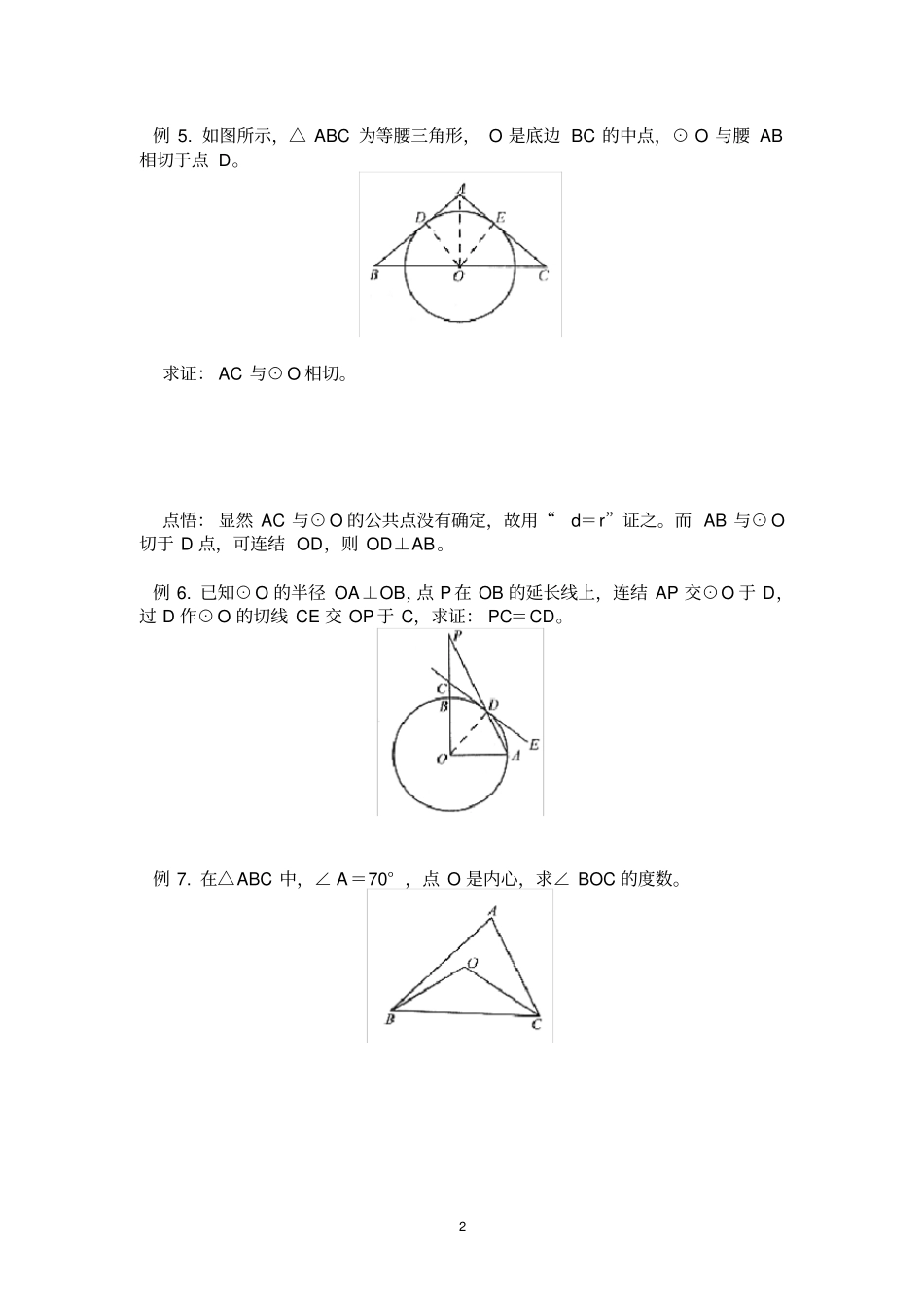
1 圆切线问题典型问题例 1. 已知半径为 3 的⊙ O 上一点 P 和圆外一点 Q,如果 OQ=5,PQ=4,则 PQ和圆的位置关系是()A. 相交B. 相切C. 相离D. 位置不定例 2. 在△ABC 中,∠ C=90° ,∠ B=30° , O 为 AB 上一点, AO=m,⊙ O的半径,问 m 在什么范围内取值时, AC 与圆:(1) 相离;( 2)相切;( 3)相交。例 3. 已知:在△ ABC 中, AD 为∠ BAC 的平分线,以 C 为圆心, CD 为半径的半圆交 BC 的延长线于点 E,交 AD 于点 F,交 AE 于点 M,且∠ B=∠CAE,FE:FD=4:3。求证: AF=DF;例 4. 已知⊙ O 中,AB 是直径,过 B 点作⊙ O 的切线,连结 CO,若 AD ∥OC交⊙ O 于 D,求证: CD 是⊙ O 的切线。2 例 5. 如图所示,△ ABC 为等腰三角形, O 是底边 BC 的中点,⊙ O 与腰 AB相切于点 D。求证: AC 与⊙ O 相切。点悟: 显然 AC 与⊙ O 的公共点没有确定,故用“d=r”证之。而 AB 与⊙ O切于 D 点,可连结 OD,则 OD⊥AB。例 6. 已知⊙ O 的半径 OA⊥OB,点 P 在 OB 的延长线上,连结 AP 交⊙O 于 D,过 D 作⊙ O 的切线 CE 交 OP 于 C,求证: PC=CD。例 7. 在△ABC 中,∠ A=70° ,点 O 是内心,求∠ BOC 的度数。3 圆切线问题典型问题答案例 1 解: OP=3,PQ=4,OQ=5,∴,∴△ OPQ 是直角三角形,且∠ OPQ=90° , ∴PQ⊥OP。即圆心 O 到 PQ 的距离等于圆的半径。∴PQ 和圆的位置关系相切,故选B。点拨: 在没有明确知道圆心到直线的距离和半径的关系时,通过已有的知识进行推证。 本题也可以通过切线的判定定理求解,即通过半径的外端并且垂直于这条半径的直线是圆的切线。例 2.点悟: 要判定直线与圆的位置关系,只要比较圆心到直线的距离与半径的大小。解: 如图所示,过 O 作 OD⊥AC 垂足为 D,,∴(1)当,即,也即时,则 AC 与⊙O 相离;(2)当,即,也即时, AC 与⊙ O 相切;(3)当,即,也即时, AC 与⊙ O 相交。例 3.证明: AD 平分∠ BAC ,∴∠ BAD =∠ DAC 。 ∠ B=∠ CAE,∴∠ BAD +∠ B=∠DAC +∠ CAE ∠ ADE=∠ BAD +∠B,∴∠ ADE =∠DAE ,∴ EA=ED DE 是半圆 C 的直径∴∠ DFE=90° ∴ AF =DF 例 4. 点悟:要证 CD 是⊙ O 的切线,须证...