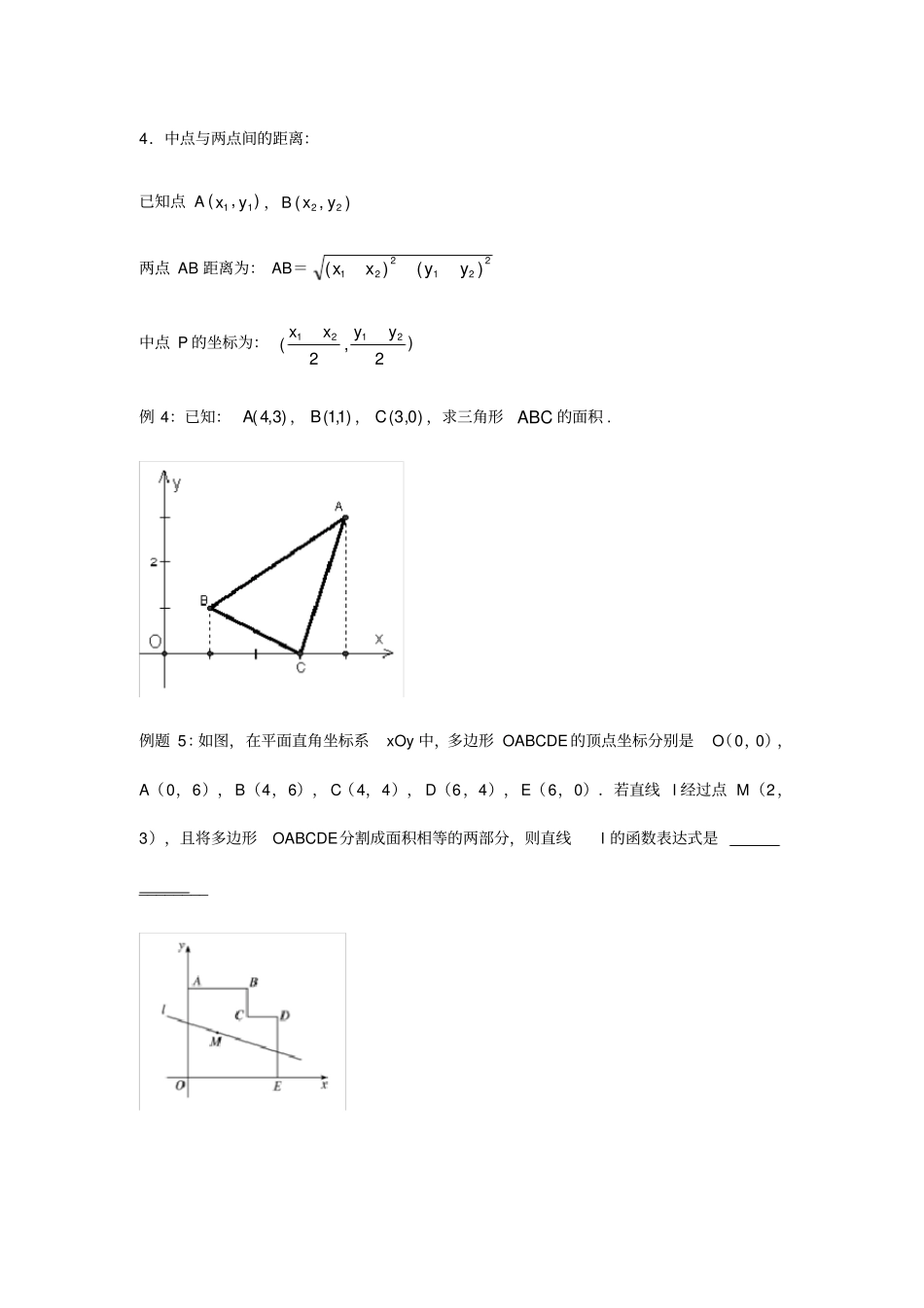
平面直角坐标系知识点梳理1.定义:平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。要求:画平面直角坐标系时,轴、y 轴上的单位长度通常应相同,但在实际应用中,有时会遇到取相同的单位长度有困难的情况,这时可灵活规定单位长度,但必须注意的是,同一坐标轴上相同长度的线段表示的单位数量相同。2.各个象限内点的特征: 第一象限:(+,+)点P(x, y),则 x>0, y>0;第二象限:(-,+)点P(x, y),则 x<0, y>0;第三象限:(-,-)点P(x, y),则 x<0, y<0;第四象限:(+,-)点P(x, y),则 x>0, y<0;四个象限的特点:第一象限(正,正),第二象限(负,正),第三象限(负,负),第四象限(正,负)在 x 轴上:( x,0)点 P( x,y),则 y=0;在 x 轴的正半轴:(+,0)点 P(x, y),则 x>0, y= 0;在 x 轴的负半轴:(-,0)点 P(x, y),则 x<0, y= 0;在 y 轴上:( 0,y)点 P( x,y),则 x= 0;在 y 轴的正半轴:( 0,+)点 P(x, y),则 x=0, y> 0;在 y 轴的负半轴:( 0,-)点 P(x, y),则 x=0, y< 0;坐标原点:( 0,0)点 P(x, y),则 x=0,y=0;例 1:已知点)5,114(2nmmM,则点 M 在平面直角坐标系中的什么位置?3. 点到坐标轴的距离:点 P(x,y)到 x 轴的距离为 |y| ,到 y 轴的距离为 |x| 。到坐标原点的距离为22yx(由勾股定理可得)例 2:已知:)3,4(A,)1,1(B,)0,3(C,求三角形 ABC 的面积 . 例 3:已知:)54,21(aaA,且点 A 到两坐标轴的距离相等,求A 点坐标.4.中点与两点间的距离:已知点 A),(11 yx,B),(22 yx两点 AB 距离为: AB=221221)()(yyxx中点 P 的坐标为:)2,2(2121yyxx例 4:已知:)3,4(A,)1,1(B,)0,3(C,求三角形 ABC 的面积 . 例题 5:如图,在平面直角坐标系xOy 中,多边形 OABCDE 的顶点坐标分别是O(0,0),A(0,6),B(4,6), C(4,4), D(6,4),E(6,0).若直线l 经过点 M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l 的函数表达式是________ 5.点的对称:点 P(m ,n) ,关于 x 轴的对称点坐标是(m,- n),关于 y 轴的对称点坐标是(-m,n) 关于原点的对称点坐标是(-m,- n) 例题 6:点 A(- 1,2)关于 y 轴的对称点坐...