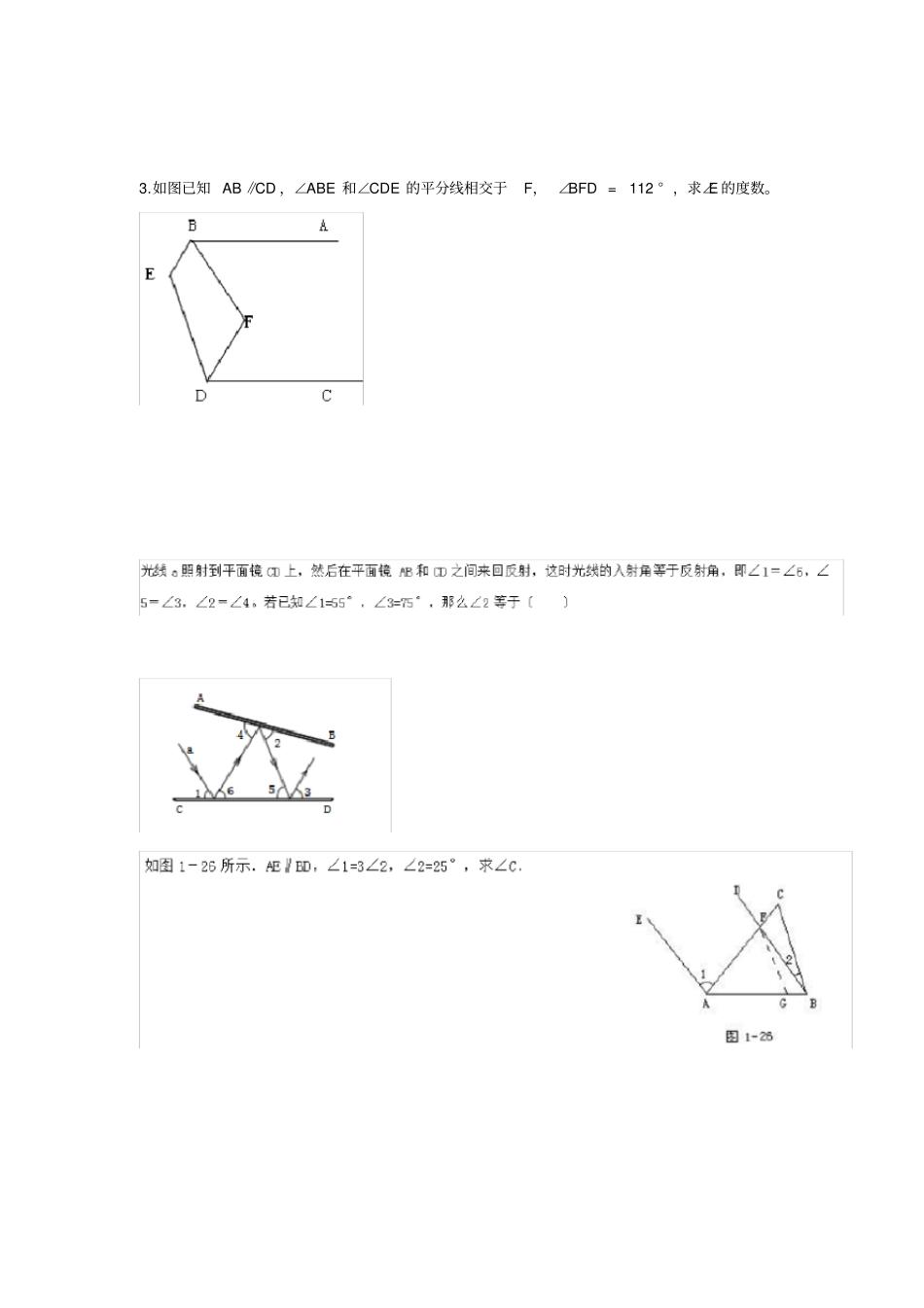
相交线与平行线拔高题1、如图,折叠宽度相等的长方形纸条,若∠1=63 ° ,则∠2= ()度2、如图,已知射线CB∥OA ,∠C= ∠OAB=100° ,E、 F 在 CB 上,且满足∠ FOB= ∠AOB ,OE 平分∠COF (1 )求∠EOB 的度数 . (2 )若平行移动AB,那么∠ OBC :∠OFC 的值是否随之发生变化?若变化,?找出变化规律;若不变,求出这个比值. (3 )在平行移动AB 的过程中,是否存在某种情况,使∠OEC= ∠OBA ?若存在,求出其度数;若不存在,说明理由. 3.如图已知 AB ∥CD ,∠ABE 和∠CDE 的平分线相交于F, ∠BFD = 112 ° ,求∠E 的度数。1、54 2、解 :(1) 因为 CB∥OA ,∠C= ∠OAB=100° ,所以∠COA=180° -100 °=80 ° ,又因为 E、F 在 CB 上,∠FOB= ∠AOB ,OE 平分∠COF ,所以∠EOB=∠COA=×80 °=40 ° . (2 )不变,因为 CB∥OA ,所以∠CBO= ∠BOA ,又∠FOB= ∠AOB ,所以∠FOB= ∠OBC ,而∠FOB+ ∠OBC= ∠OFC,即∠OFC=2 ∠OBC ,所以∠OBC :∠OFC=1 :2. (3 )存在某种情况,使∠OEC= ∠OBA ,此时∠OEC= ∠OBA=60 °. 理由如下:因为 ∠COE+ ∠CEO+ ∠C=180 ° ,∠BOA+ ∠OAB+ ∠ABO=180° ,且∠OEC= ∠OBA ,∠C= ∠OAB=100° ,所以∠COE = ∠BOA ,又因为∠ FOB= ∠AOB ,OE 平分∠COF ,所以∠BOA= ∠BOF= ∠FOE= ∠EOC=∠COA=20 ° ,所以∠OEC= ∠OBA=60 ° . 解:作 GE∥AB ,FH ∥CD ∴∠ABF= ∠BFH ∠HFD= ∠CDF ∵FB 为∠ABE 的平分线∴∠ABF= ∠FBE=∠ABE ∵FD 为∠CDE 的平分线∴∠CDF= ∠EDF=∠CDE ∵∠BFD = 112 °∴∠ABE+ ∠CDE=2 ∠ABF+2 ∠CDF=2 ∠BFH+2 ∠HFD=2 ∠BFD ∴∠ABE+ ∠CDE=2 ×112 °=224 °∵AB ∥CD ∴ EG∥CD ∴∠ABE+ ∠BEG=180 ° ∠CDE+ ∠GED=180 °∴ABE+ ∠BEG+ ∠CDE+ ∠GED=360 ° ∴∠BEG+ ∠GED=136 °