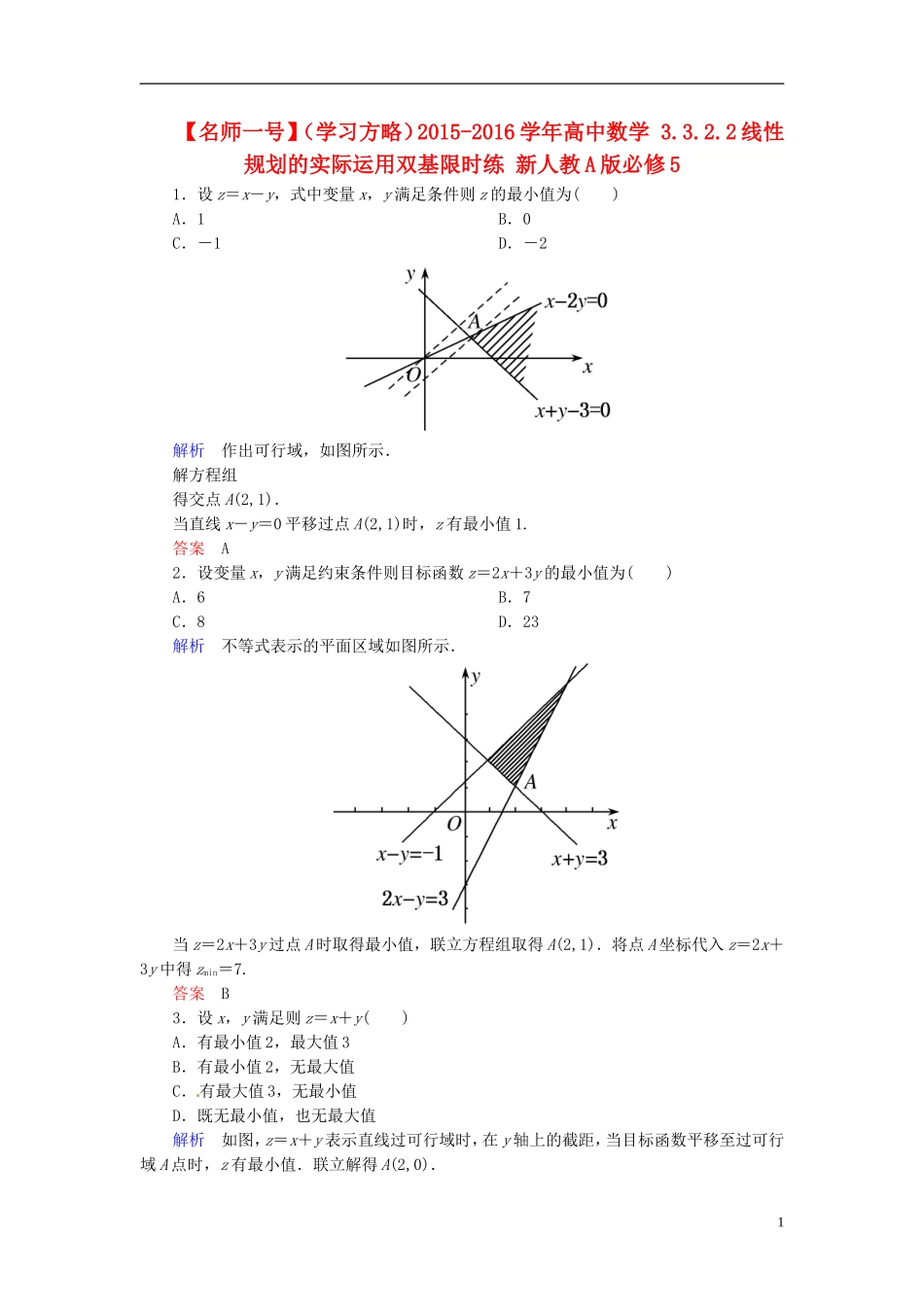
【名师一号】(学习方略)2015-2016 学年高中数学 3.3.2.2 线性规划的实际运用双基限时练 新人教 A 版必修 51.设 z=x-y,式中变量 x,y 满足条件则 z 的最小值为( )A.1 B.0C.-1 D.-2解析 作出可行域,如图所示.解方程组得交点 A(2,1).当直线 x-y=0 平移过点 A(2,1)时,z 有最小值 1.答案 A2.设变量 x,y 满足约束条件则目标函数 z=2x+3y 的最小值为( )A.6 B.7C.8 D.23解析 不等式表示的平面区域如图所示.当 z=2x+3y 过点 A 时取得最小值,联立方程组取得 A(2,1).将点 A 坐标代入 z=2x+3y 中得 zmin=7.答案 B3.设 x,y 满足则 z=x+y( )A.有最小值 2,最大值 3B.有最小值 2,无最大值C.有最大值 3,无最小值D.既无最小值,也无最大值解析 如图,z=x+y 表示直线过可行域时,在 y 轴上的截距,当目标函数平移至过可行域 A 点时,z 有最小值.联立解得 A(2,0).1z 最小值=2,z 无最大值.答案 B4.某企业生产甲、乙两种产品.已知生产每吨甲产品要用 A 原料 3 吨、 B 原料 2 吨;生产每吨乙产品要用 A 原料 1 吨、B 原料 3 吨.销售每吨甲产品可获得利润5 万元、每吨乙产品可获得利润 3 万元.该企业在一个生产周期内消耗 A 原料不超过 13 吨、B 原料不超过 18 吨,那么该企业可获得最大利润是( )A.12 万元 B.20 万元C.25 万元 D.27 万元解析 设该企业在一个生产周期内生产甲产品 x 吨,乙产品 y 吨,获得利润 z 万元,则依题意,有目标函数 z=5x+3y,画出不等式组表示的平面区域及直线 l0:5x+3y=0,易知当平移l0经过点(3,4)时,z 取得最大值为 5×3+3×4=27,故选 D.答案 D5.某公司租赁甲、乙两种设备生产 A,B 两类产品,甲种设备每天能生产 A 类产品 5 件和B 类产品 10 件,乙种设备每天能生产 A 类产品 6 件和 B 类产品 20 件.已知设备甲每天的租赁费用为 200 元,设备乙每天的租赁费用为 300 元.现该公司至少要生产 A 类产品 50 件,B 类产品 140 件,所需租赁费最少为________元.解析 设租赁甲、乙两种设备 x,y 台,则目标函数 z=200x+300y,画出可行域知目标函数在点(4,5)处取得最小值,故目标函数的最小值为 2300.答案 23006.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在下表中,那么为...