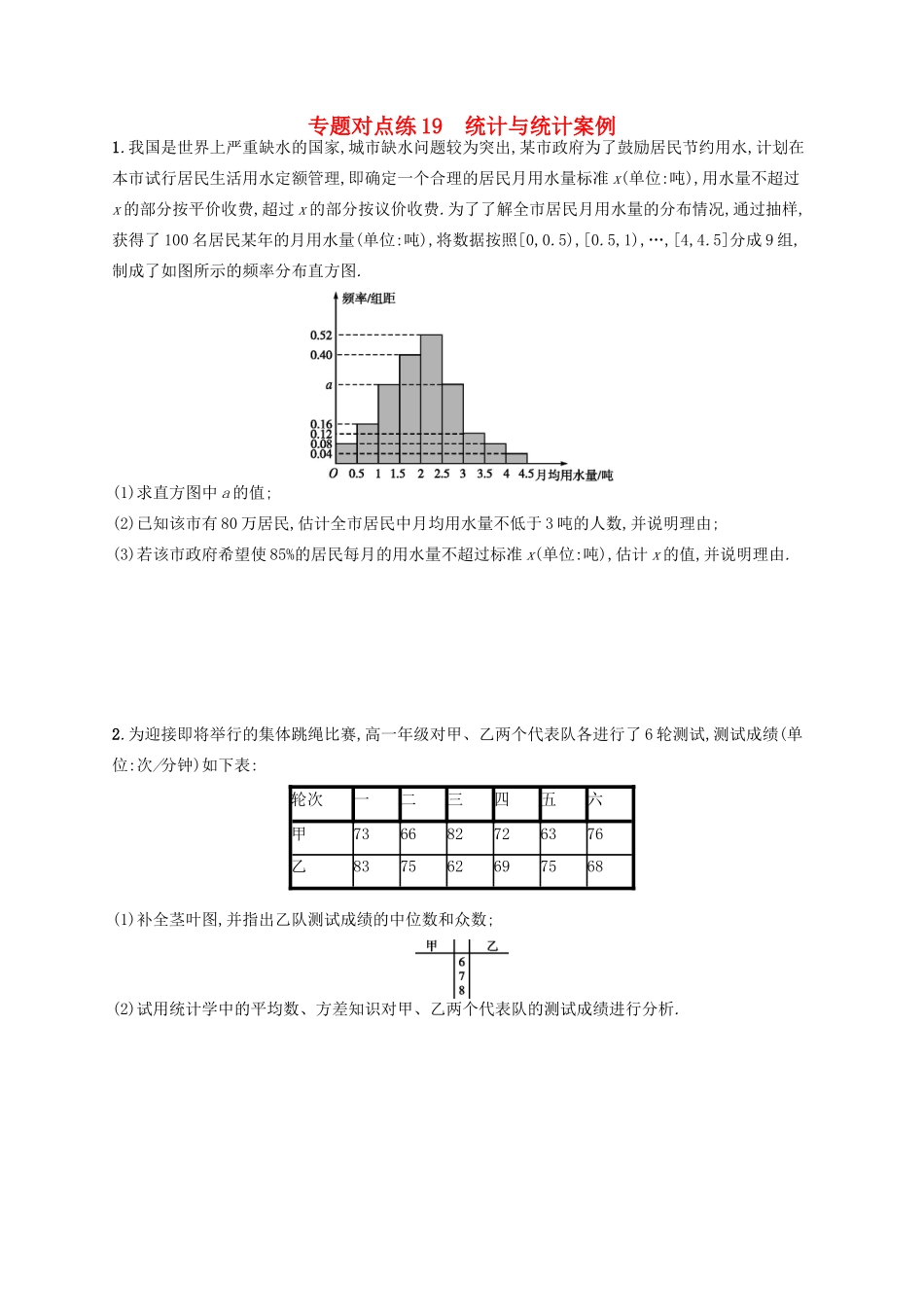
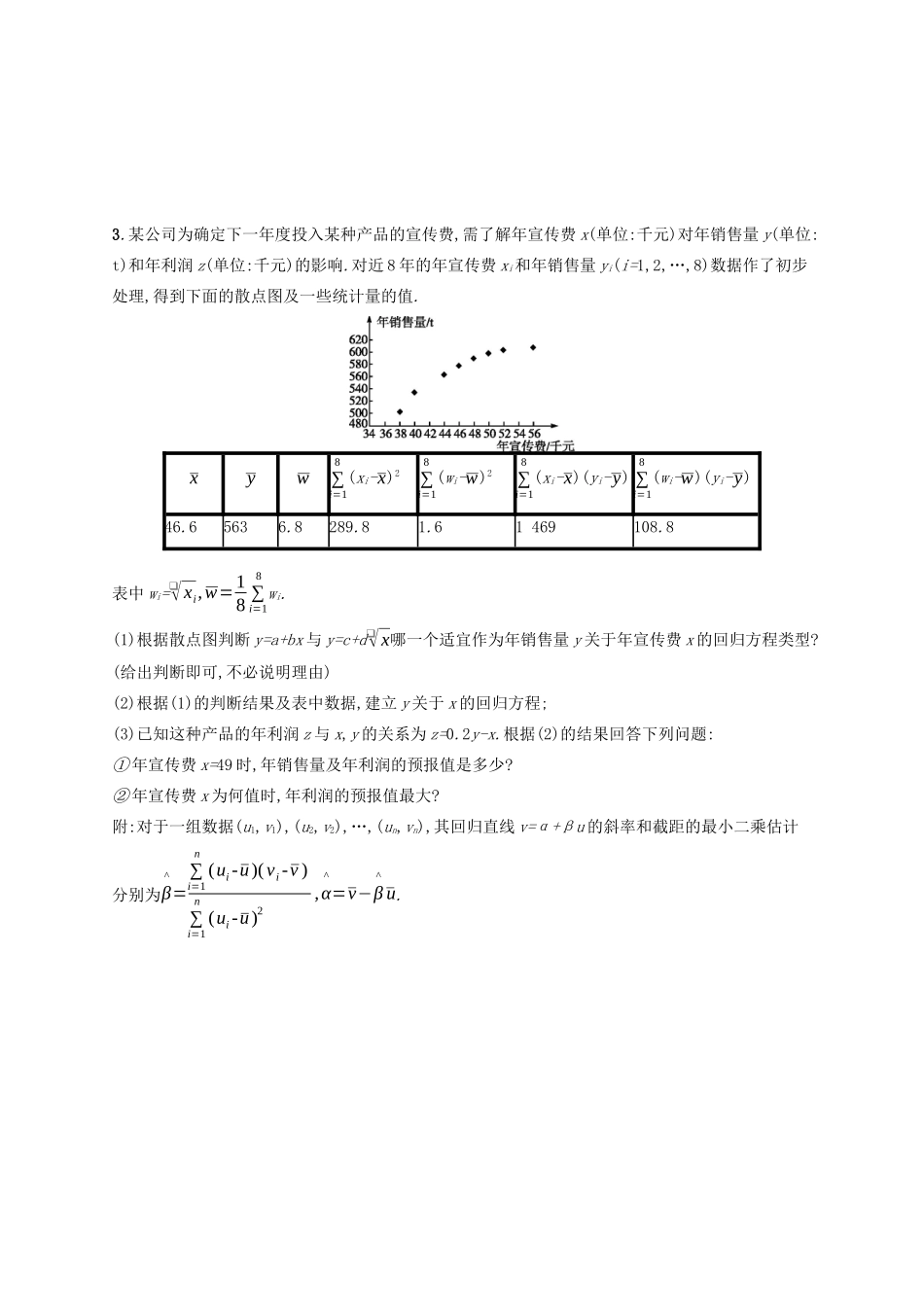
专题对点练 19 统计与统计案例1.我国是世界上严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准 x(单位:吨),用水量不超过x 的部分按平价收费,超过 x 的部分按议价收费.为了了解全市居民月用水量的分布情况,通过抽样,获得了 100 名居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成 9 组,制成了如图所示的频率分布直方图.(1)求直方图中 a 的值;(2)已知该市有 80 万居民,估计全市居民中月均用水量不低于 3 吨的人数,并说明理由;(3)若该市政府希望使 85%的居民每月的用水量不超过标准 x(单位:吨),估计 x 的值,并说明理由.2.为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了 6 轮测试,测试成绩(单位:次/分钟)如下表:轮次一二三四五六甲736682726376乙837562697568(1)补全茎叶图,并指出乙队测试成绩的中位数和众数;(2)试用统计学中的平均数、方差知识对甲、乙两个代表队的测试成绩进行分析.3.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 x(单位:千元)对年销售量 y(单位:t)和年利润 z(单位:千元)的影响.对近 8 年的年宣传费 xi和年销售量 yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.xyw∑i=18(xi-x)2∑i=18(wi-w)2∑i=18(xi-x)(yi-y) ∑i=18(wi-w)(yi-y)46.65636.8289.81.61 469108.8表中 wi=❑√ xi,w=18 ∑i=18wi.(1)根据散点图判断 y=a+bx 与 y=c+d❑√ x哪一个适宜作为年销售量 y 关于年宣传费 x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立 y 关于 x 的回归方程;(3)已知这种产品的年利润 z 与 x,y 的关系为 z=0.2y-x.根据(2)的结果回答下列问题:① 年宣传费 x=49 时,年销售量及年利润的预报值是多少?② 年宣传费 x 为何值时,年利润的预报值最大?附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线 v=α+βu 的斜率和截距的最小二乘估计分别为β^=∑i=1n(ui-u)(vi-v )∑i=1n(ui-u)2,α^=v−β^u.4.某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在 30 分以下的学生后,共有男生 300 名,女生 200 名.现采用分层抽样的方法,从中抽取了 100 名学生,按性别分为两组,并将两组学生成绩分为...