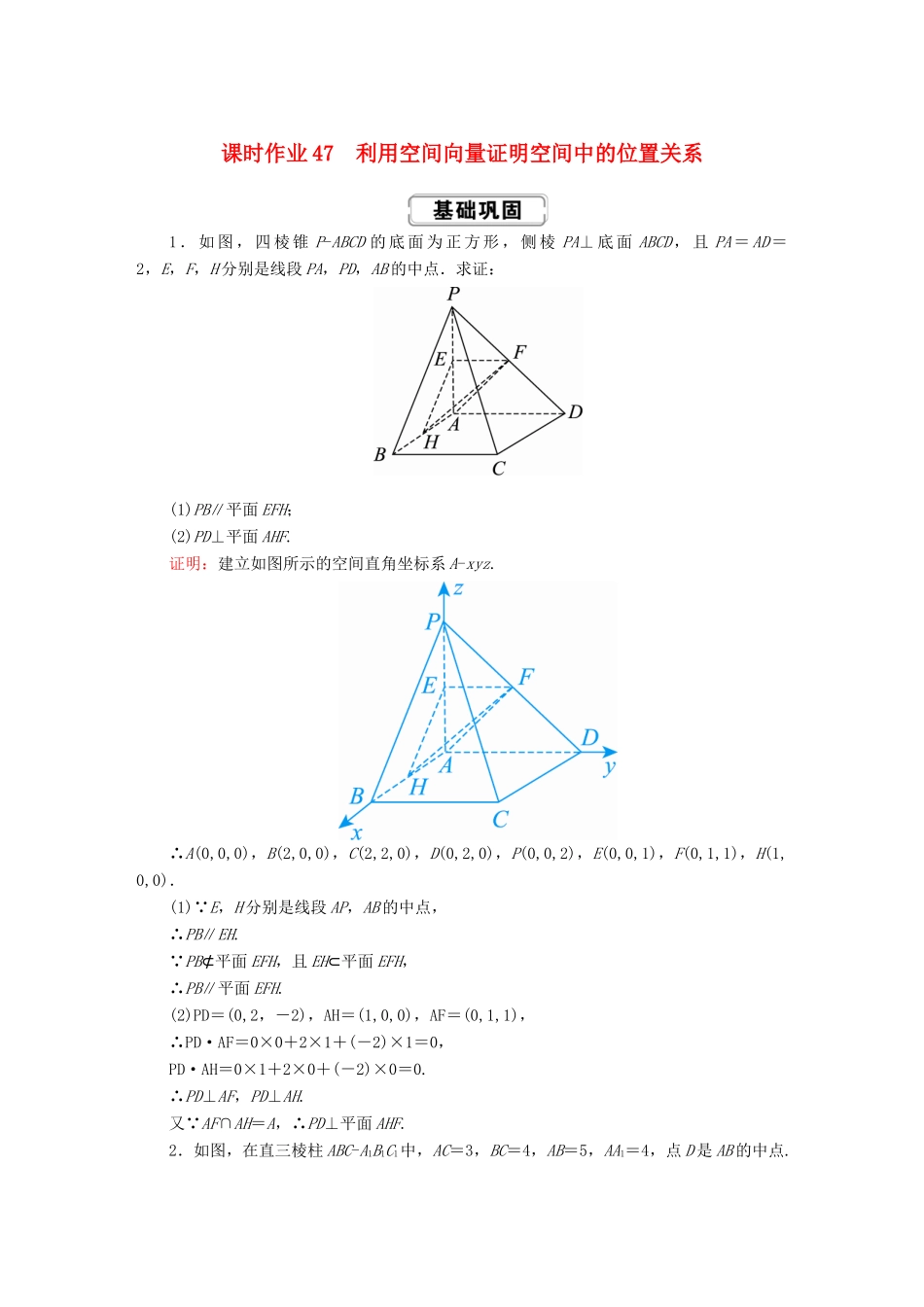
课时作业 47 利用空间向量证明空间中的位置关系1 . 如 图 , 四 棱 锥 P-ABCD 的 底 面 为 正 方 形 , 侧 棱 PA⊥ 底 面 ABCD , 且 PA = AD =2,E,F,H 分别是线段 PA,PD,AB 的中点.求证:(1)PB∥平面 EFH;(2)PD⊥平面 AHF.证明:建立如图所示的空间直角坐标系 A-xyz.∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),H(1,0,0).(1) E,H 分别是线段 AP,AB 的中点,∴PB∥EH. PB⊄平面 EFH,且 EH⊂平面 EFH,∴PB∥平面 EFH.(2)PD=(0,2,-2),AH=(1,0,0),AF=(0,1,1),∴PD·AF=0×0+2×1+(-2)×1=0,PD·AH=0×1+2×0+(-2)×0=0.∴PD⊥AF,PD⊥AH.又 AF∩AH=A,∴PD⊥平面 AHF.2.如图,在直三棱柱 ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点 D 是 AB 的中点.(1)证明 AC⊥BC1;(2)证明 AC1∥平面 CDB1.证明:因为直三棱柱 ABC-A1B1C1的底面边长分别为 AC=3,BC=4,AB=5,所以△ABC为直角三角形,AC⊥BC.所以 AC,BC,C1C 两两垂直.如图,以 C 为坐标原点,直线 CA,CB,CC1分别为 x 轴,y 轴,z 轴建立空间直角坐标系,则 C(0,0,0),A(3,0,0),B(0,4,0),C1(0,0,4),A1(3,0,4),B1(0,4,4),D.(1)因为AC=(-3,0,0),BC1=(0,-4,4),所以AC·BC1=0,所以 AC⊥BC1.(2)设 CB1与 C1B 的交点为 E,连接 DE,则 E(0,2,2),DE=,AC1=(-3,0,4),所以DE=AC1,DE∥AC1.因为 DE⊂平面 CDB1,AC1⊄平面 CDB1,所以 AC1∥平面 CDB1.3.如图,在三棱柱 ABC-A1B1C1 中,AA1C1C 是边长为 4 的正方形.平面 ABC⊥平面AA1C1C,AB=3,BC=5.(1)求证:AA1⊥平面 ABC;(2)证明:在线段 BC1上存在点 D,使得 AD⊥A1B,并求的值.证明:(1)因为 AA1C1C 为正方形,所以 AA1⊥AC.因为平面 ABC⊥平面 AA1C1C,AA1⊂平面 AA1C1C,且 AA1垂直于这两个平面的交线 AC,所以 AA1⊥平面 ABC.(2)由(1)知 AA1⊥AB,AA1⊥AC.由题知 AB=3,BC=5,AC=4,所以 AB⊥AC.如图,以 A 为原点建立空间直角坐标系 A-xyz,则 B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4).设 D(x,y,z)是直线 BC1上的一点,且BD=λBC1,所以(x,y-3,z)=λ(4,-3,4),解得 x=4λ,y=3-3λ,z=4λ,所以AD=(4λ,3-3λ,4λ).由AD·A1B=0,A1B=(0,3,-4),则 9-25λ=0,解得 λ=.因为∈[0,1],所以...