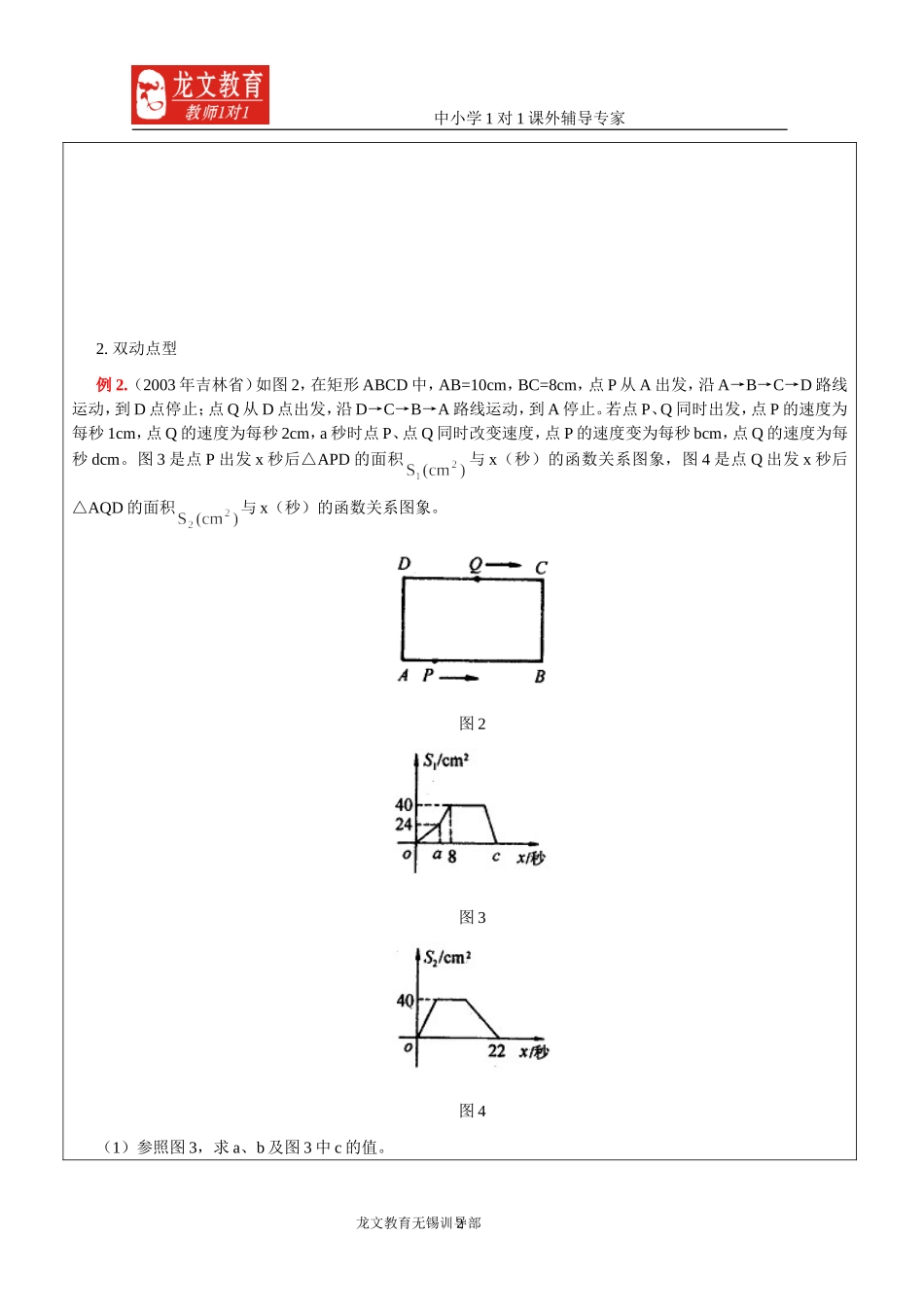
中小学1对1课外辅导专家龙文教育学科导学案教师:田勇健学生:徐博源日期:2011-星期:时段:课题动态几何问题学习目标与考点分析动态几何题目的常考类型和针对不同类型的解题方法学习重点分类总结对应的一般解题方法,学会如何去思考学习方法归纳总结,例题讲解学习内容与过程知识点梳理动态几何题已成为中考试题的一大热点题型。在近几年各地的中考试卷中,以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中,考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力。解决动态几何题的策略是:把握运动规律,寻求运动中的特殊位置;在“动”中求“静”,在“静”中探求“动”的一般规律。通过探索、归纳、猜想,获得图形在运动过程中是否保留或具有某种性质。题型分类:点动型、线动型、面动型运动形式:平移、旋转、翻折、滚动特别:点动型就是在三角形、矩形、梯形等一些几何图形上,设计一个或几个动点,并对这些点在运动变化的过程中产生的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究。解决此类动点几何问题常常用的是“类比发现法”,也就是通过对两个或几个相类似的数学研究对象的异同,进行观察和比较,从一个容易探索的研究对象所具有的性质入手,去猜想另一个或几个类似图形所具有的类似性质,从而获得相关结论。类比发现法大致可遵循如下步骤:(1)根据已知条件,先从动态的角度去分析观察可能出现的情况;(2)结合某一相应图形,以静制动,运用所学知识(常见的有三角形全等、三角形相似等)得出相关结论。(3)类比猜想出其他情况中的图形所具有的性质。一.动点型1.单动点型例1.如图1,在矩形ABCD中,AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PF⊥AC,E,F分别是垂足,求PE+PF的长。龙文教育无锡训导部1中小学1对1课外辅导专家2.双动点型例2.(2003年吉林省)如图2,在矩形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A路线运动,到A停止。若点P、Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度为每秒dcm。图3是点P出发x秒后△APD的面积与x(秒)的函数关系图象,图4是点Q出发x秒后△AQD的面积与x(秒)的函数关系图象。图2图3图4(1)参照图3,求a、b及图3中c的值。龙文教育无锡训导部2中小学1对1课外辅导专家(2)求d的值。(3)设点P离开点A的路程为,点Q到点A还需走的路程为,请分别写出动点P、Q改变速度后,、与出发后的运动时间x(秒)的函数关系式。并求出P、Q相遇时x的值。(4)当点Q出发________秒时,点P、点Q在运动路线上相距的路程为25cm。分析与略解:解决此类问题的关键是应注意图形位置变化及动点运动的时间和速度,用分类讨论的思想来求解。二.动线型1.线平移型例3.(2004年河南省)如图5,边长为2的正方形ABCD中,顶点A的坐标是(0,2),一次函数y=x+t的图象L随t的不同取值变化时,位于L的右下方由L和正方形的边围成的图形面积为S(阴影部分)。(1)当t取何值时,S=3?(2)在平面直角坐标系下,画出S与t的函数图象。2.线旋转型例4.(2004年海口市)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。(1)当直线MN绕点C旋转到图6的位置时,求证:①△ADC≌△CEB;②DE=AD+BE。龙文教育无锡训导部3中小学1对1课外辅导专家图6(2)当直线MN绕点C旋转到图7的位置时,求证:DE=。图7(3)直线MN绕点C旋转到图8的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明。图8三.动面型1.面平移型例5.(2001年吉林省)如图9,有一边长为5cm的正方形ABCD和等腰△PQR,PQ=PR=5cm,QR=8cm,点B、C、Q、R在同一条直线L上,当C、Q两点重合时,等腰△PQR以1cm/s的速度沿直线L按箭头所示方向开始龙文教育无锡训导部4中小学1对1课外辅导专家匀速运动,ts后正方形ABCD与等腰△PQR重合部分的面积为。解答下列问题:(1)当t=3s时,求S的值;(2)当t=5s时,求S的值;(3)当时,求S与t的函数关...