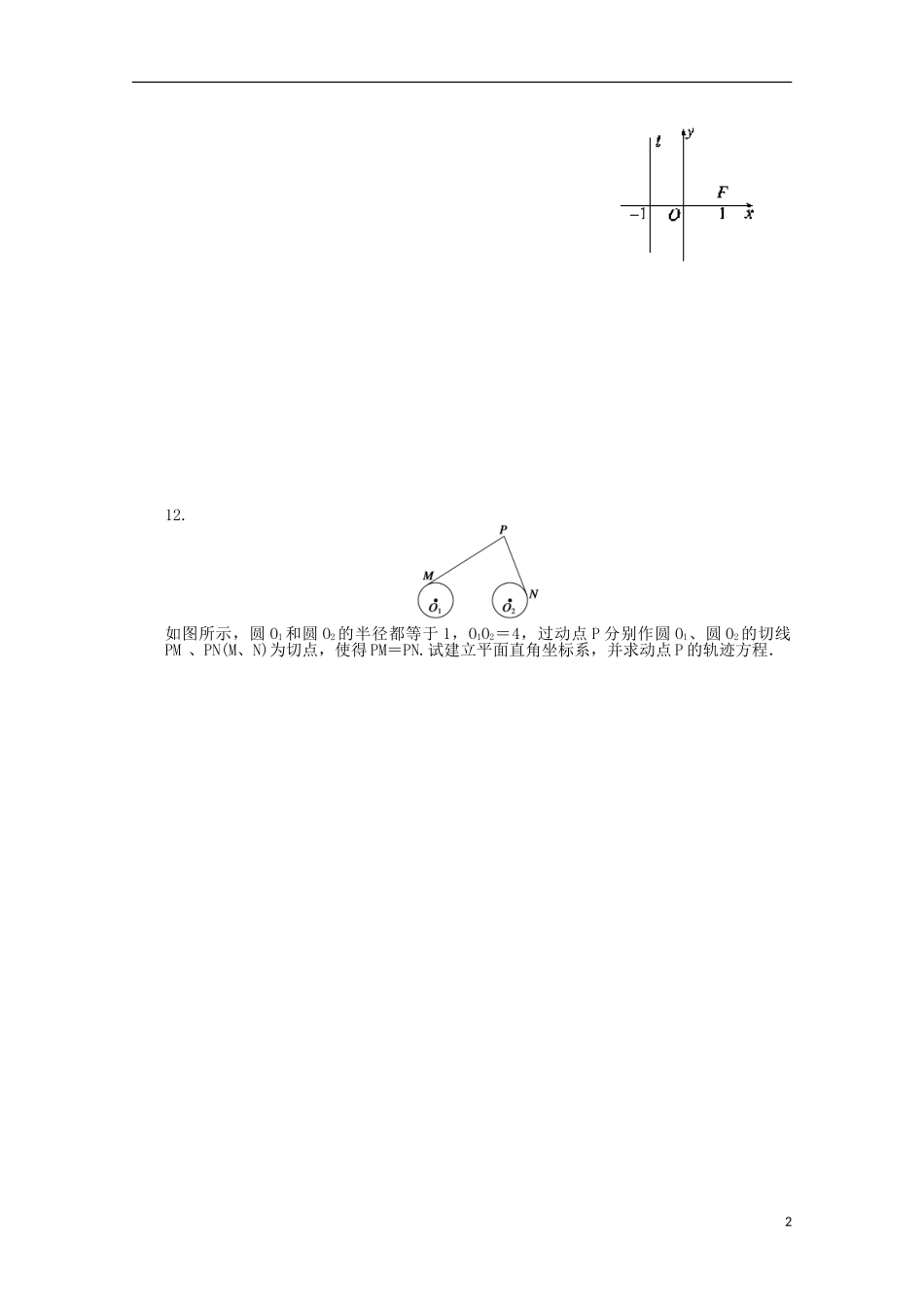
2.6.2 求曲线的方程课时目标 1.掌握求轨迹方程建立坐标系的一般方法,熟悉求曲线方程的五个步骤.2.掌握求轨迹方程的几种常用方法.1.求曲线方程的一般步骤(1)建立适当的____________;(2)设曲线上任意一点 M 的坐标为(x,y);(3)列出符合条件 p(M)的方程 f(x,y)=0;(4)化方程 f(x,y)=0 为____________;(5)证明以化简后的方程的解为坐标的点都在曲线上.2.求曲线方程(轨迹方程)的常用方法有直接法、代入法、定义法、参数法、待定系数法.一、填空题1.已知点 A(-2,0),B(2,0),C(0,3),则△ABC 底边 AB 的中线的方程是______________.2.与点 A(-1,0)和点 B(1,0)的连线的斜率之积为-1 的动点 P 的轨迹方程是______________.3.与圆 x2+y2-4x=0 外切,又与 y 轴相切的圆的圆心轨迹方程是____________________.4.抛物线的顶点在原点,对称轴重合于椭圆 9x2+4y2=36 短轴所在的直线,抛物线焦点到顶点的距离为 3,则抛物线的方程为____________.5.设过点 P(x,y)的直线分别与 x 轴的正半轴和 y 轴的正半轴交与 A、B 两点,点 Q 与点 P关于 y 轴对称,O 为坐标原点,若=2PA,且OQ·AB=1,则 P 点的轨迹方程是________________________.6.到直线 x-y=0 与 2x+y=0 距离相等的动点轨迹方程是________________.7.方程(x+y-1)=0 表示的曲线是____________________________.8.直角坐标平面 xOy 中,若定点 A(1,2)与动点 P(x,y)满足OP·OA=4,则点 P 的轨迹方程是__________________________.二、解答题9.设圆 C:(x-1)2+y2=1,过原点 O 作圆 C 的任意弦,求所作弦的中点的轨迹方程.10.已知△ABC 的两顶点 A、B 的坐标分别为 A(0,0),B(6,0),顶点 C 在曲线 y=x2+3 上运动,求△ABC 重心的轨迹方程.能力提升11.如图,已知点 F(1,0),直线 l:x=-1,P 为平面上的动点,过 P 作直线 l 的垂线,垂足为点 Q,且QP·QF=FP·FQ.求动点 P 的轨迹 C 的方程.112.如图所示,圆 O1 和圆 O2 的半径都等于 1,O1O2=4,过动点 P 分别作圆 O1、圆 O2 的切线PM 、PN(M、N)为切点,使得 PM=PN.试建立平面直角坐标系,并求动点 P 的轨迹方程.21.求轨迹方程的五个步骤:建系、设点、列式、化简、证明.2.明确求轨迹和求轨迹方程的不同.3.求出轨迹方程时,易忽视对变量的限制条件,在化简变形的过程中若出现了非等价变形...