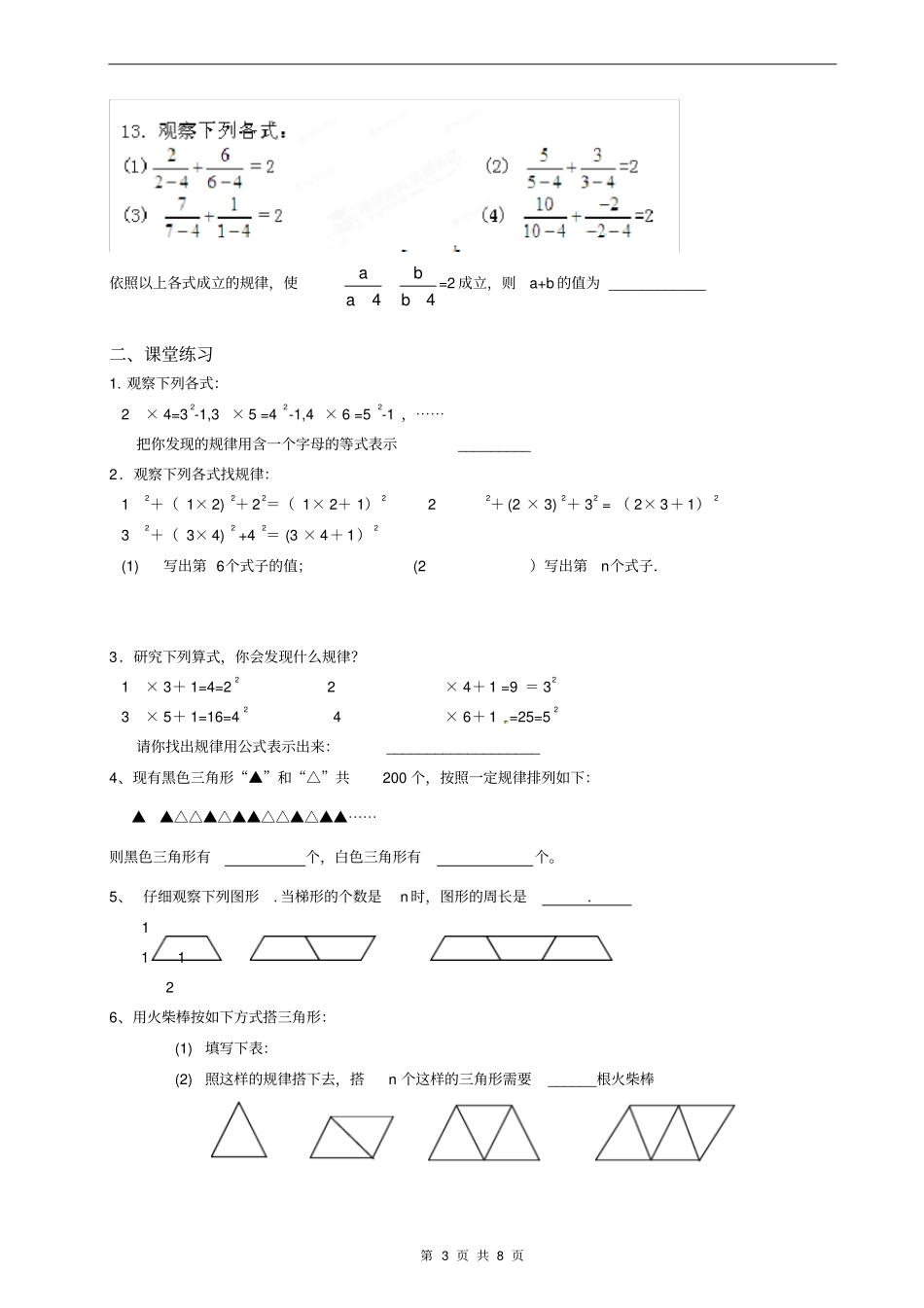
第 1 页 共 8 页一、例题讲解1. 观察下面的每列数,按某种规律在横线上适当的数。 (1)-23, -18 , -13,______, ____ ____ ; ; (2)2345,,,816 3264, _______ , _________ ;2.有一组数:1,2,5,10,17,26,.....,请观察这组数的构成规律,用你发现的规律确定第8个数为 __________. 3.观察下列算式:21=2,22 =4,23 =8,24= 16,25 =32,26=64,27= 128 ,通过观察,用你所发现的规律确定22011的个位数字是()A. 2 B. 4 C. 6 D. 8 4.一根 lm长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第六次后剩下的绳子的长度为() A.31()2m B. 51( )2m C. 61( )2m D. 121( )2m 5. 下面一组按规律排列的数:1,2,4,8,16.......,第 2011 个数应是() A. 22011 B. 22011-1 C.22010 D.以上答案不对6 .观察,寻找规律( 1) 0.12= ________ , 12= _________ , 102= __________ , 1002= ___________ ; (2)0.13=_________ , 13= _________ , 103= __________ , 1003= ___________ ;观察结果,你发现什么了?7.观察下列三行数:第一行:-1,2 , -3,4, -5 ⋯⋯第二行:1,4,9, 16,25 ,⋯⋯第三行:0,3,8,15,24,⋯⋯ (1)第一行数按什么规律排列? (2)第二行、第三行分别与第一行数有什么关系? (3)取每行的第10个数,计算这三个数的和.第 2 页 共 8 页8.有规律排列的一列数:2,4,6,8,10,12,⋯⋯它的每一项可用式子2n(n 是正整数) 表示.有规律排列的一列数:1, -2,3 , -4,5 , -6,7 , -8...... (1)它的每一项你认为可用怎样的式子来表示? (2)它的第 100 个数是多少? (3)2012是不是这列数中的数?如果是,是第几个数?9.先完成下列计算: 1× 9+ 2= 11; 12 × 9+ 3= ________ ; 123 × 9 + 4=__________;⋯⋯你能说出得数的规律吗?请你根据发现的算式的规律求出1234567 × 9 + 8的值.10.如果 1+2-3-4+5+6-7-8 +9+⋯⋯,是从1开始的连续整数中依次两个取正,两个取负写下去的一串数,则前2012 个数的和是多少?11.观察下列各式:12+1=1 × 2 22+2=2 × 3 32+3=3 × 4 请把你猜想到的规律用自然数n表示出来___________________ 12.老师在黑板上写出三个等式: 52-32=8× 2,92-72= 8× 4, 152-32=8× 27 王华接着又写了两个具有同样规律的算式:...