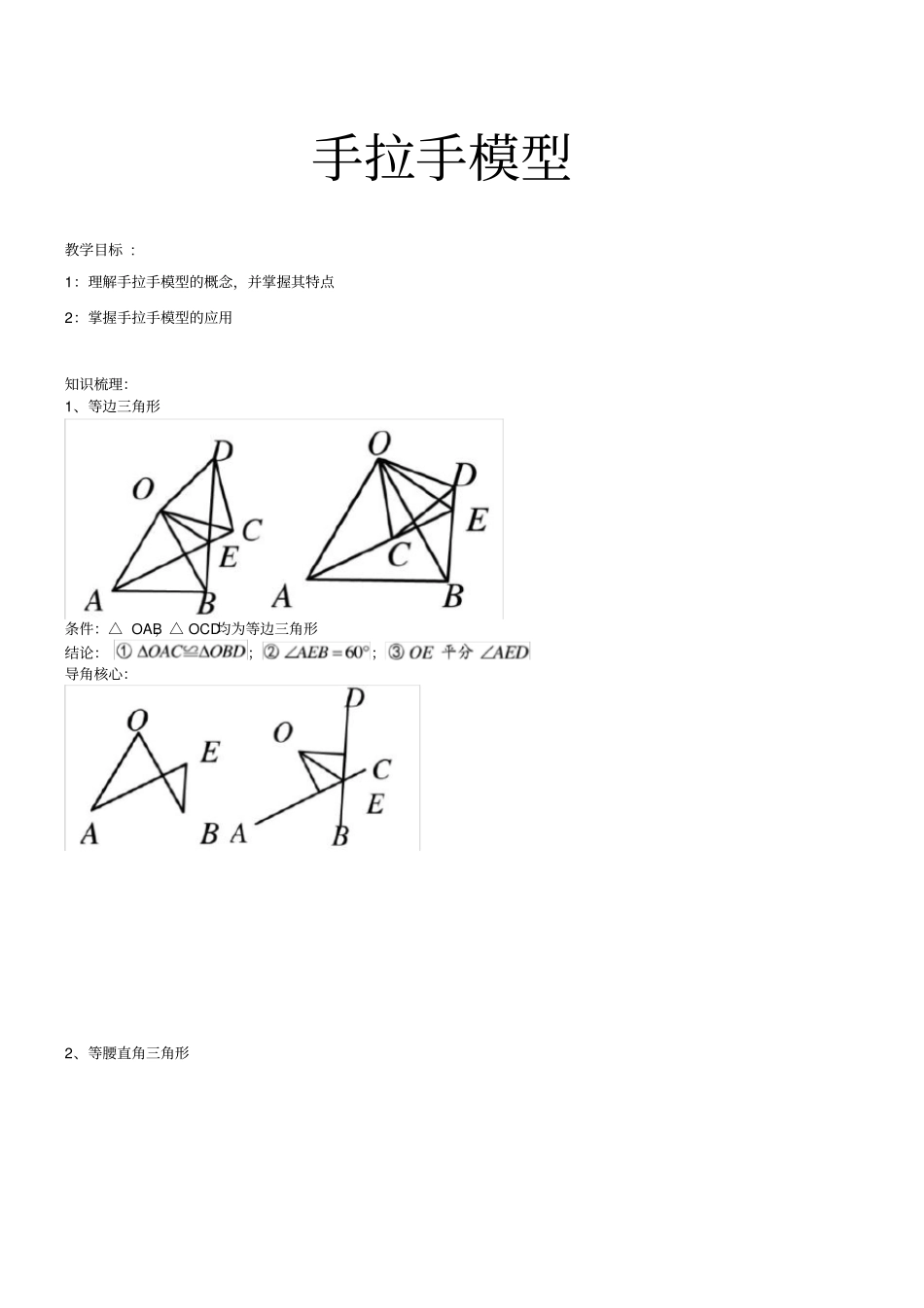
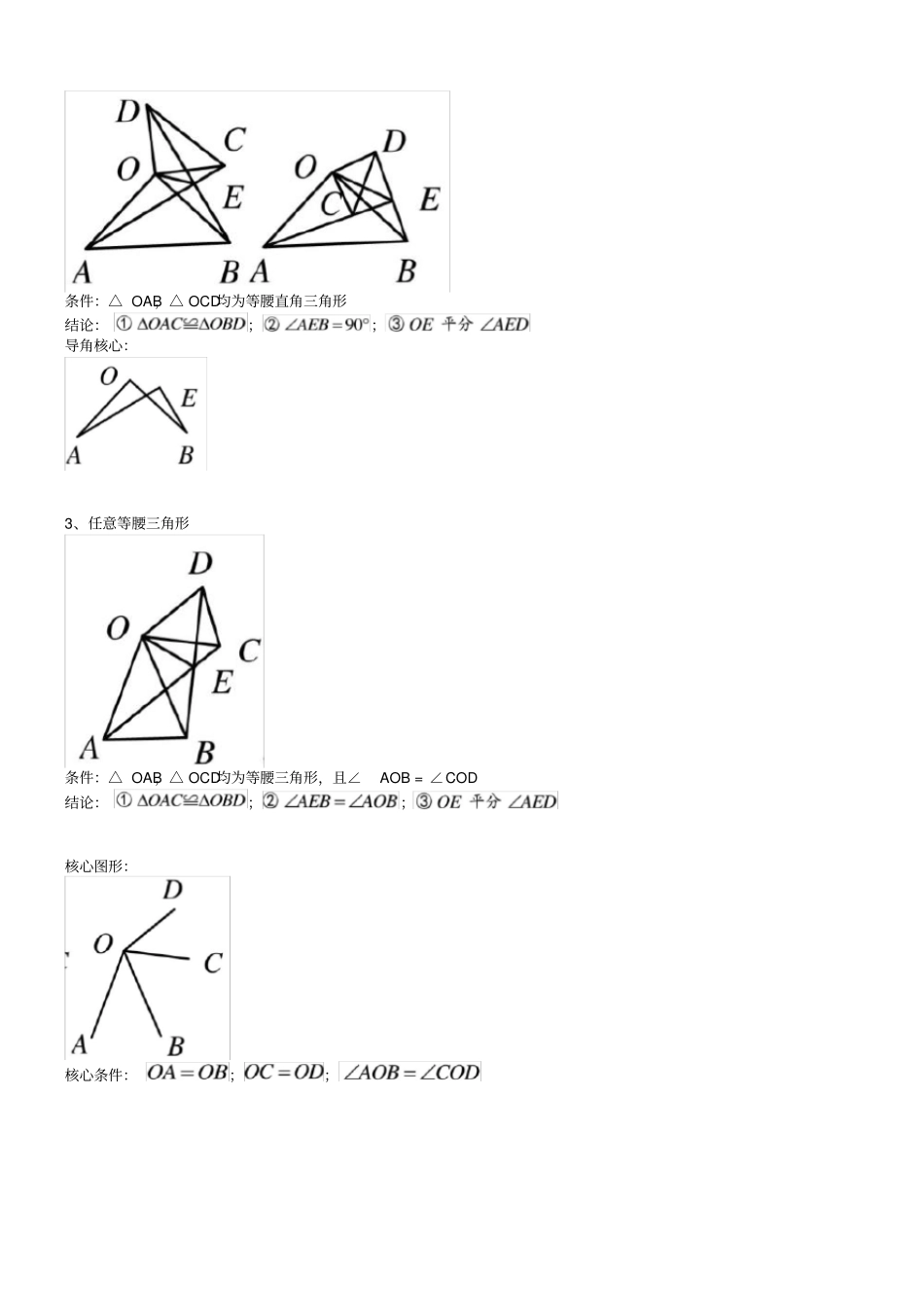
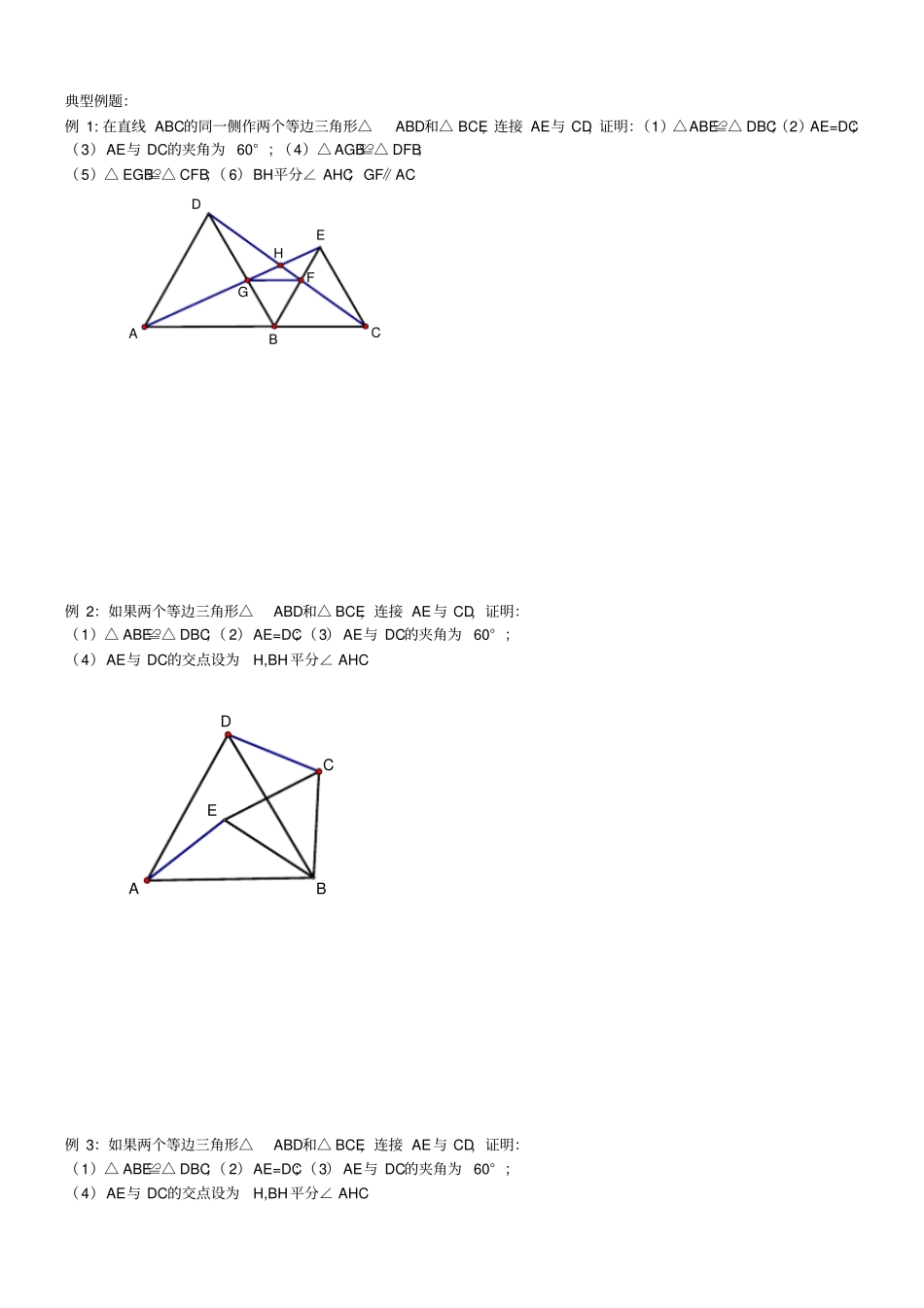
手拉手模型教学目标 : 1:理解手拉手模型的概念,并掌握其特点2:掌握手拉手模型的应用知识梳理:1、等边三角形条件:△ OAB,△ OCD均为等边三角形结论:;;导角核心:2、等腰直角三角形条件:△ OAB,△ OCD均为等腰直角三角形结论:;;导角核心:3、任意等腰三角形条件:△ OAB,△ OCD均为等腰三角形,且∠AOB = ∠COD 结论:;;核心图形:核心条件:;;典型例题:例 1: 在直线 ABC的同一侧作两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ABE≌△ DBC;(2)AE=DC;(3)AE与 DC的夹角为 60° ;(4)△ AGB≌△ DFB;(5)△ EGB≌△ CFB;( 6)BH平分∠ AHC;GF∥AC HFGEDABC例 2:如果两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ ABE≌△ DBC;( 2)AE=DC;(3) AE与 DC的夹角为 60° ;(4)AE与 DC的交点设为H,BH平分∠ AHC EBDAC例 3:如果两个等边三角形△ABD和△ BCE,连接 AE与 CD,证明:(1)△ ABE≌△ DBC;( 2)AE=DC;(3) AE与 DC的夹角为 60° ;(4)AE与 DC的交点设为H,BH平分∠ AHC HEBDAC例 4:如图,两个正方形ABCD和 DEFG,连接 AG与 CE,二者相交于H 问:(1)△ ADG≌△ CDE是否成立?( 2)AG是否与 CE相等?(3)AG与 CE之间的夹角为多少度?(4) HD是否平分∠ AHE?HEFADBCG例 5:如图两个等腰直角三角形ADC与 EDG,连接 AG,CE,二者相交于H.问 ( 1)△ ADG≌△ CDE是否成立?( 2)AG是否与 CE相等?(3)AG与 CE之间的夹角为多少度?(4) HD是否平分∠ AHE?HGADCE例 6:两个等腰三角形ABD与 BCE,其中 AB=BD,CB=EB,∠ABD=∠CBE,连接 AE与 CD. 问( 1)△ ABE≌△ DBC是否成立?(2)AE是否与 CD相等?( 3)AE与 CD之间的夹角为多少度?(4)HB是否平分∠ AHC?HDABCE例 7:如图,分别以△ ABC 的边 AB、AC 同时向外作等腰直角三角形,其中 AB =AE ,AC =AD,∠BAE =∠CAD=90° ,点 G为 BC中点,点 F 为 BE 中点,点 H 为 CD中点。探索GF 与 GH 的位置及数量关系并说明理由。例 8:如图 1,已知∠ DAC=90° ,△ ABC是等边三角形,点P 为射线 AD任意一点( P与 A 不重合),连结 CP,将线段 CP绕点 C顺时针旋转60° 得到线段CQ,连结 QB并延长交直线AD于点 E. (1)如图 1,猜想∠ QEP=_______° ;( 2)如图 2, 3...