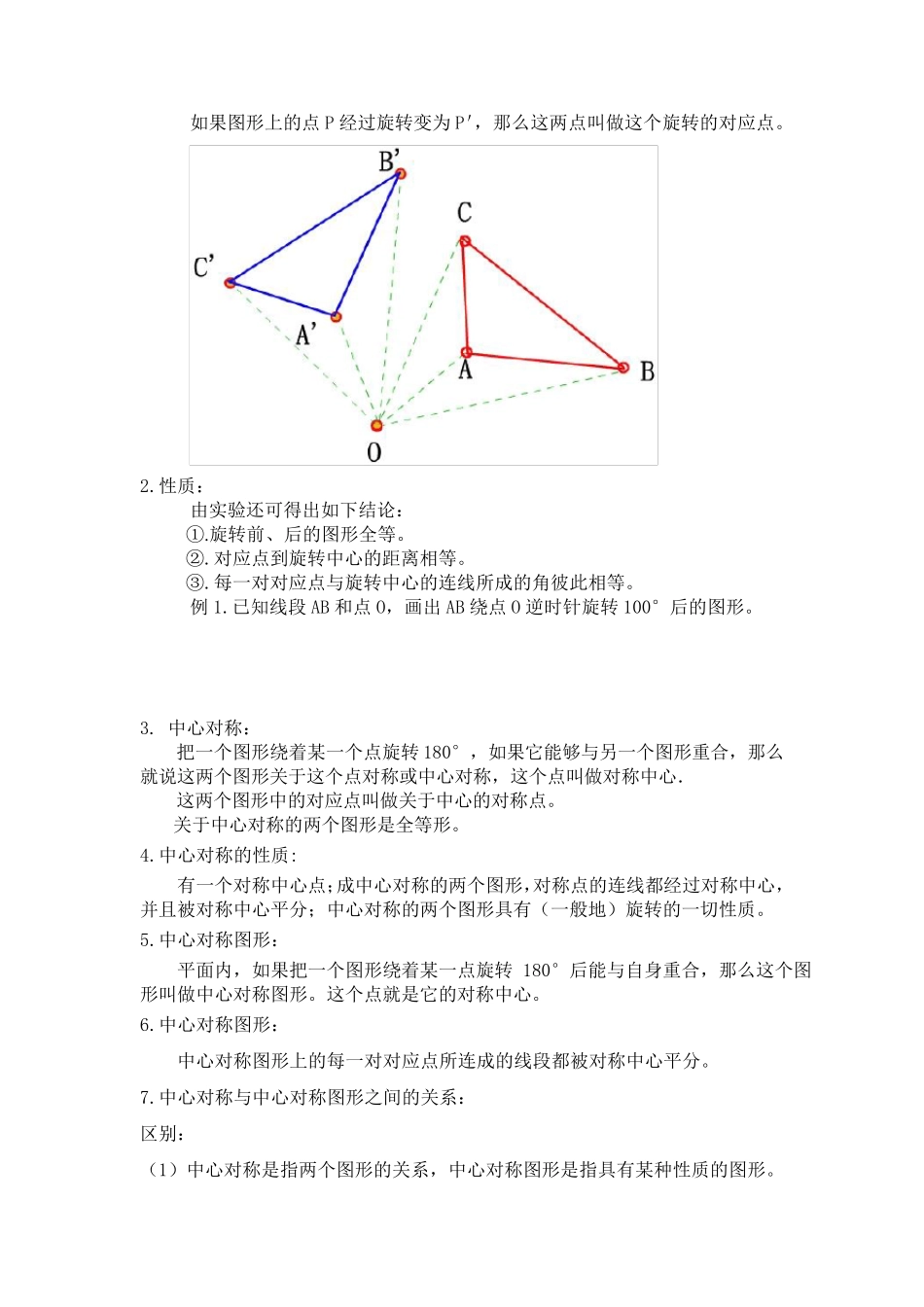
中心对称及中心对称图形专题讲义 一、基本概念: 1.图形的旋转: ⑴ .定义:在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转。 这个定点称为旋转中心。 旋转的角度称为旋转角。 如果图形上的点P 经过旋转变为P',那么这两点叫做这个旋转的对应点。 2.性质: 由实验还可得出如下结论: ①.旋转前、后的图形全等。 ②.对应点到旋转中心的距离相等。 ③.每一对对应点与旋转中心的连线所成的角彼此相等。 例1.已知线段AB 和点O,画出AB 绕点O 逆时针旋转100°后的图形。 3. 中心对称: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心. 这两个图形中的对应点叫做关于中心的对称点。 关于中心对称的两个图形是全等形。 4.中心对称的性质: 有一个对称中心点;成中心对称的两个图形,对称点的连线都经过对称中心,并且被对称中心平分;中心对称的两个图形具有(一般地)旋转的一切性质。 5.中心对称图形: 平面内,如果把一个图形绕着某一点旋转180°后能与自身重合,那么这个图形叫做中心对称图形。这个点就是它的对称中心。 6.中心对称图形: 中心对称图形上的每一对对应点所连成的线段都被对称中心平分。 7.中心对称与中心对称图形之间的关系: 区别: (1)中心对称是指两个图形的关系,中心对称图形是指具有某种性质的图形。 (2)成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上。 联系: 若把中心对称图形的两部分看成两个图形,则它们成中心对称;若把中心对称的两个图形看成一个整体,则成为中心对称图形。 8.轴对称图形与中心对称图形: 轴对称图形 中心对称图形 有一条对称轴 直线 有一个对称中心 点 沿对称轴对折 绕对称中心旋转180° 对折后与原图形重合 旋转180°后与原图形重合 9.轴对称与中心对称: 轴对称 中心对称 有一条对称轴 直线 有一个对称中心 点 图形沿对称轴对折(翻转180°)后重合 图形绕对称中心旋转180°后重合 对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分 【中心对称和中心对称图形基础练习】 1.判断题 (1)三角形一定不是中心对称图形 ( ) (2)中心对称图形的对称中心是唯一的 ( ) (3)如果一个四边形是中心对称图形,那么这个四边形一定是平行四边形 ( )...