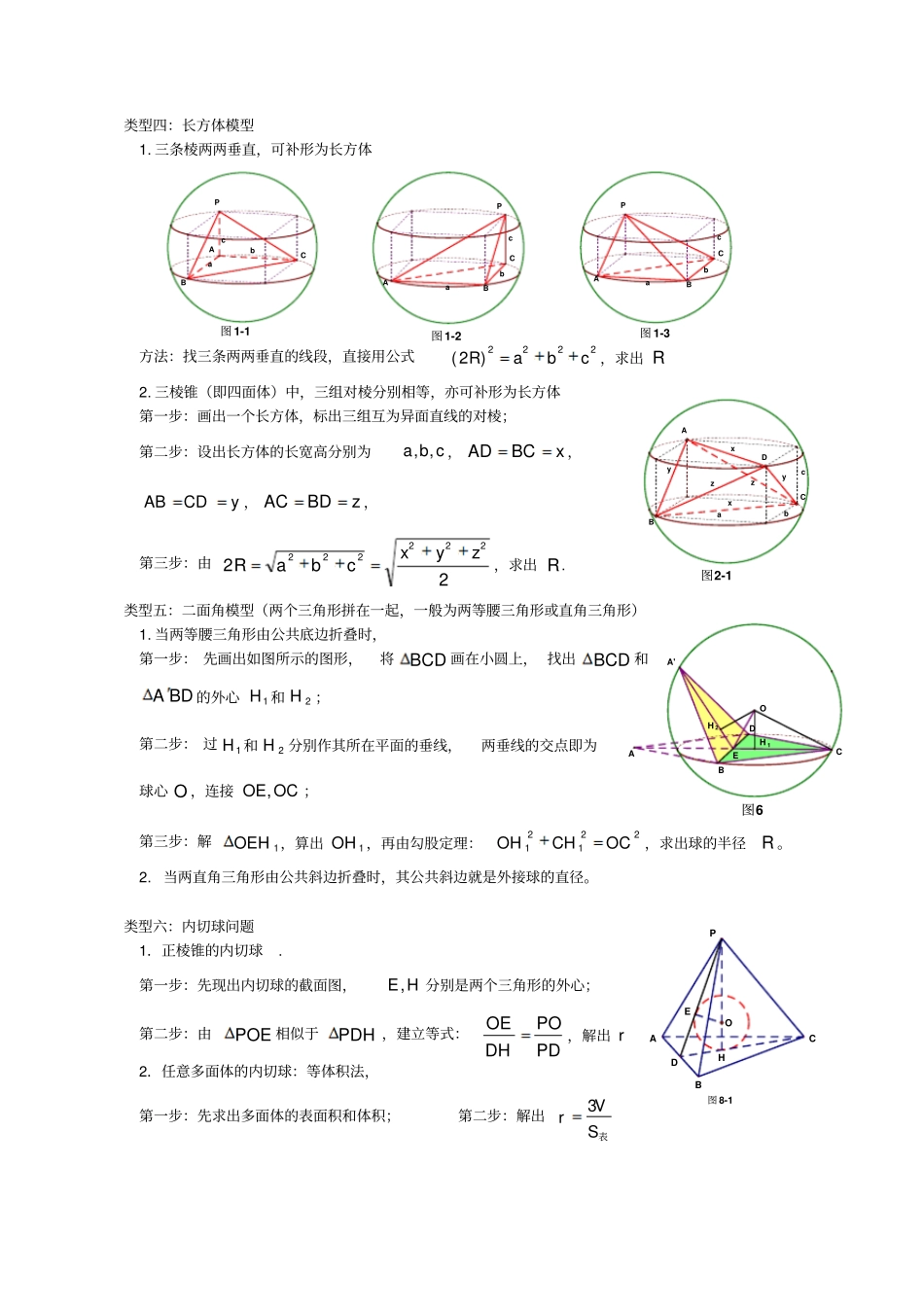
图 5ADPO1OCB图 5-4PADO1OCB图3-1C1B1AEFA1O 1OO2BC专题 3 搞定空间几何体的外接球与内切球一、基本方法:(1)定心:确定球心,构造直角三角形利用正余弦定理及勾股定理求解(222drR);该方法是解决外接球问题的主要的通法,但对空间想象能力、作图能力要求较高;所以熟悉以下的几种模型才能准确快速的解决外接球问题。(2)补形:补成长方体,利用长方体对角线求解(22224cbaR);有些几何体比较难确定球心, 而几何体刚好是长方体的一部分,其外接球与长方体的外接球是同一个球,故可利用长方体模型求解。另外有些不规则的几何体还可以选择建系,设球心, 利用球心到各顶点的距离相等求出球心坐标求解。 但该方法计算量大,高考一般不会考查。高考中以模型一、二、三、四为主。类型一:锥体模型(P 的射影是ABC 的外心即侧棱长相等)第一步:确定球心O 的位置,取ABC 的外心1O ,则1,,OOP三点共线;第二步:先算出小圆1O 的半径rAO1,再算出棱锥的高hPO1;第三步: 勾股定理:21212OOAOOA222)(rRhR,解出 R类型二:柱体模型(直棱柱、圆柱)第一步: 确定球心 O 的位置,1O 是ABC 的外心,则1OO平面 ABC ;第二步:算出小圆1O 的半径rAO1,hAAOO212111;第三步:勾股定理:21212OOAOOA222)2(rhR22)2( hrR,解出 R类型三:线面垂直模型(一条直线垂直于一个平面,柱体也可以归于该模型)第一步:将ABC 画在小圆面上,D 为小圆上任意的一点,;第二步:1O 为ABC 的外心,所以1OO平面 ABC ,算出小圆1O 的半径rDO1(三角形的外接圆直径算法:利用正弦定理,得rCcBbAa2sinsinsin),PAOOd211;第三步:利用勾股定理求三棱锥的外接球半径:222drR. 图6H 1EACOBDA'H 2类型四:长方体模型1. 三条棱两两垂直,可补形为长方体cab图 1-1CPABabc图 1-2PCBAabc图 1-3CBPA方法:找三条两两垂直的线段,直接用公式2222)2(cbaR,求出 R2. 三棱锥(即四面体)中,三组对棱分别相等,亦可补形为长方体第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为cba,,,xBCAD,yCDAB,zBDAC,第三步:由22222222zyxcbaR,求出 R. 类型五:二面角模型(两个三角形拼在一起,一般为两等腰三角形或直角三角形)1. 当两等腰三角形由公共底边折叠时,第一步: 先画出如图所示的图形,将BCD 画在小圆上, 找出BCD 和BDA的外心1H 和2H;第二步: 过1H 和2H分别作其所在平面的垂线,两...