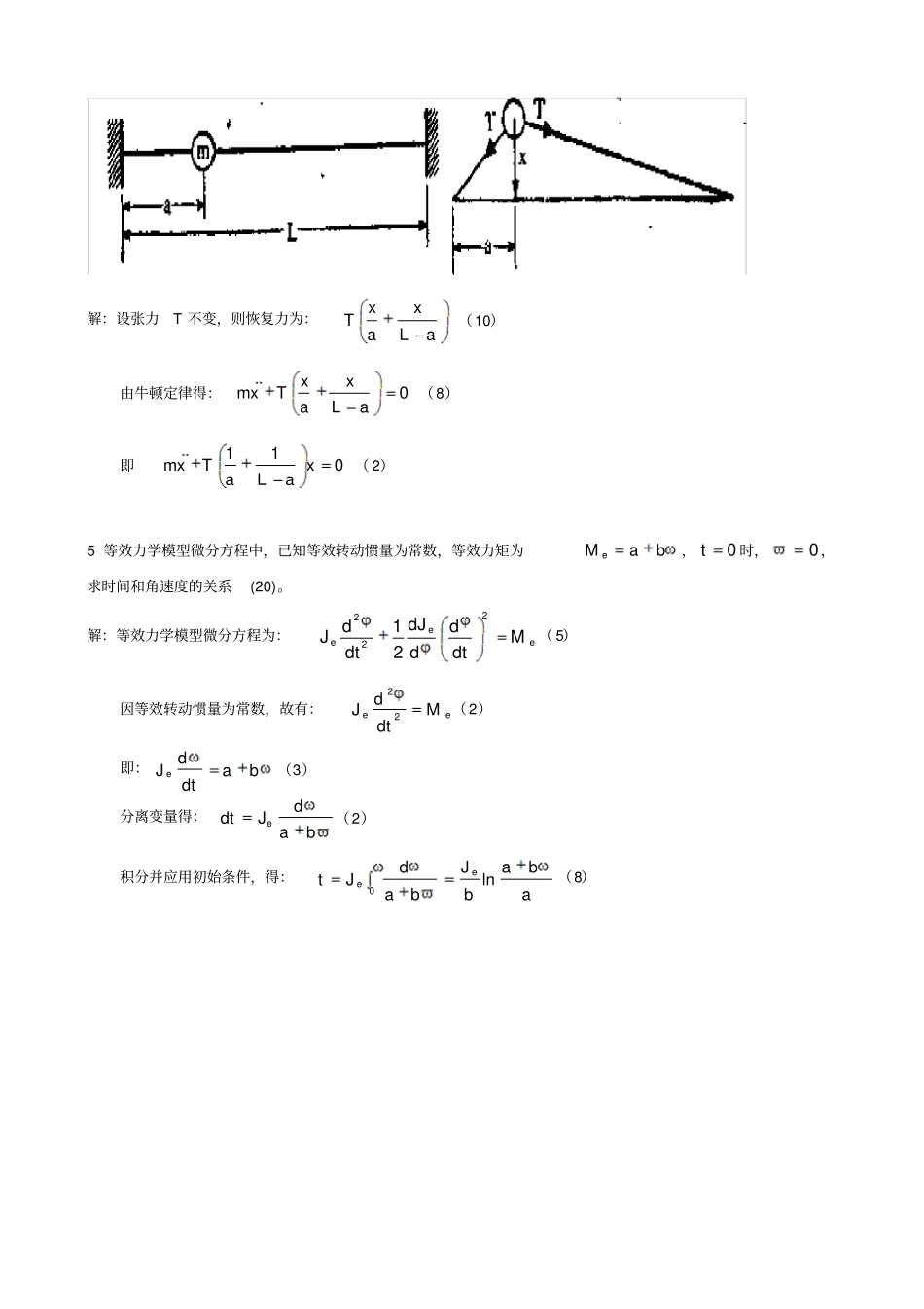
机械系统动力学试题B平分标准1 填空( 20)(每空 2分)离散线性系统的数学模型可用线性常微分方程描述。 LTI 系统为线性时不变系统。静态设计主要考虑 静态载荷作用,动态设计主要考虑振动与动态载荷作用。系统有离散系统和连续系统。确定性系统在随机激励下,响应是随机的。重力场的势函数为-mgy 。广义坐标为完全决定系统状态的独立参数。牛顿力学的主要不便是处理约束反力不方便。连续系统的自由度数为无穷多。2 用拉格朗日方程建立单摆运动方程(20)。解:0sinsin0)8()4(sin)5()3()cos1(2121)5()2()2()1(22222glmglmldtdmlEEmglVQmglVmlmvEq即所以代入方程计算广义力计算动能与势能确定广义坐标3 写出建立等效力学模型的步骤(20)。解:( 1)选取等效构件,通常选主动构件为等效构件(4);( 2)计算等效力,根据做功相等的原则进行(4);( 3)计算等效质量,根据动能相等的原则,将各个构件向等效构件进行等效(4);( 4)对等效构件列运动方程(4);( 5)解方程( 4)。4 如图,弦上有一质量m,设张力 T不变,推导微分方程(20)。解:设张力T 不变,则恢复力为:aLxaxT(10)由牛顿定律得:0aLxaxTxm(8)即011xaLaTxm( 2)5 等效力学模型微分方程中,已知等效转动惯量为常数,等效力矩为baM e,0t时,0,求时间和角速度的关系(20)。解:等效力学模型微分方程为:eeeMdtdddJdtdJ22221( 5)因等效转动惯量为常数,故有:eeMdtdJ22(2)即:badtdJ e(3)分离变量得:badJdte(2)积分并应用初始条件,得:ababJbadJteeln0(8)