数学极限的求法VIP免费

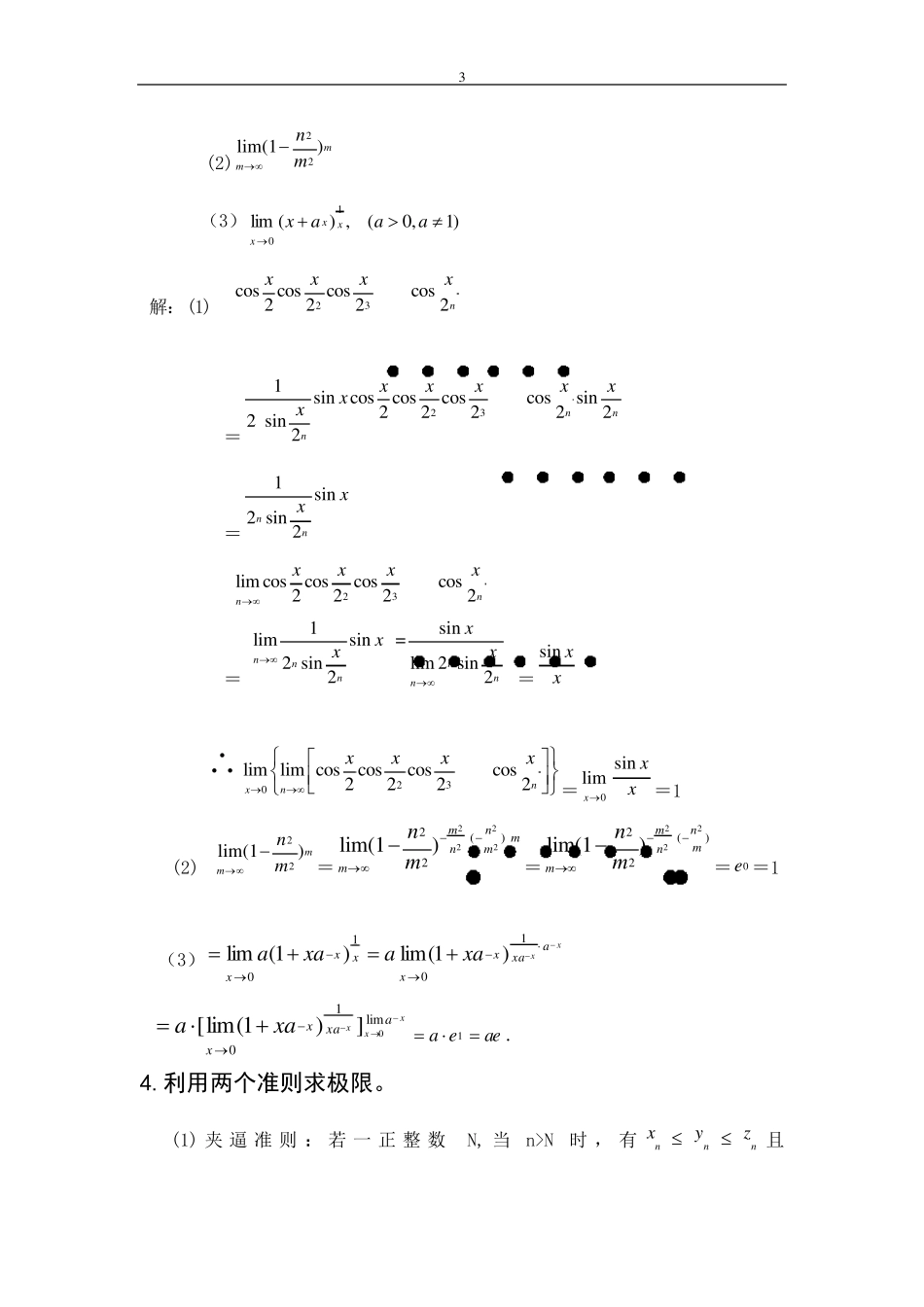
1 数学极限的求法 常见:夹逼准则, 无穷小量的性质,两个重要极限，等价无穷小，洛必达法则, 中值定理, 定积分, 泰勒展开式。后四种不常见。另外求代数式极限可参见课本 P48 上。证明极限用定义证。 1：利用等价无穷小代换求极限 当 x 趋于 0 时等价，例如 x ～xsin～xtan～xarcsin～xarctan～)1ln(x～1xe xnxaxxxxxxxxxxna1~,~1)1(,21~cos1,~arcsin,~tan,~sin2 当上面每个函数中的自变量x 换成)(xg时（0)(xg），仍有上面的等价关系成立，例如：当0x时， 13 xe ～ x3 ；)1ln(2x ～ 2x。 例：求4303lim(sin)2xxxx 解：sin 22xx 4303lim(sin)2xxxx＝ 4303lim( )2xxxx＝ 4330lim8xxxx＝8 2：利用极限的四则运算性质求极限 进行恒等变形，例如分子分母约去趋于零但不等于零的因式；分子分母有理化消除未定式；通分化简；化无穷多项的和（或积）为有限项。 例；求极限 2 (1)2211lim 21xxxx (2)312lim3xxx (3)3113lim()11xxx (4) 已知 111,1 22 3(1)nxnn求limnnx 解：(1) 2211lim 21xxxx＝1(1)(1)lim (1)(21)xxxxx=11lim 21xxx＝23 (2)（2）＝3( 12)( 12)lim(3)( 12)xxxxx＝33lim(3)( 12)xxxx＝14 (3)3113lim()11xxx ＝2312lim1xxxx＝21(1)(2)lim (1)(1)xxxxxx＝212lim1xxxx ＝-1 (4) 因为 111,1 22 3(1)nxnn 111111111122334411nnn 11n  所以 1limlim(1)1nnnxn 3：利用两个重要极限公式求极限 (1) 0sin1limlimsin1xxxxxx (2)101lim(1)lim(1)xxxxxex 例：求下列函数的极限[4] (1) 230lim lim coscoscoscos2222nnnxxxx 3 (2)22lim(1)mmnm （3）)1,0(,)(lim10aaaxxxx 解：(1) 23coscoscoscos2222nxxxx ＝231sincoscoscoscossin222222 sin 2nnnxxxxxxx ＝1sin2 sin 2nnxx 23lim coscoscoscos2222nnxxxx ＝1 limsin2 sin 2nnnxxsin =lim 2 sin 2nnnxx ＝sin xx 230lim lim coscoscoscos2222nxnxxxx＝0limxsin xx＝1 (2) 22lim(1)mmnm＝22222()2lim(1)mnmnmmn...