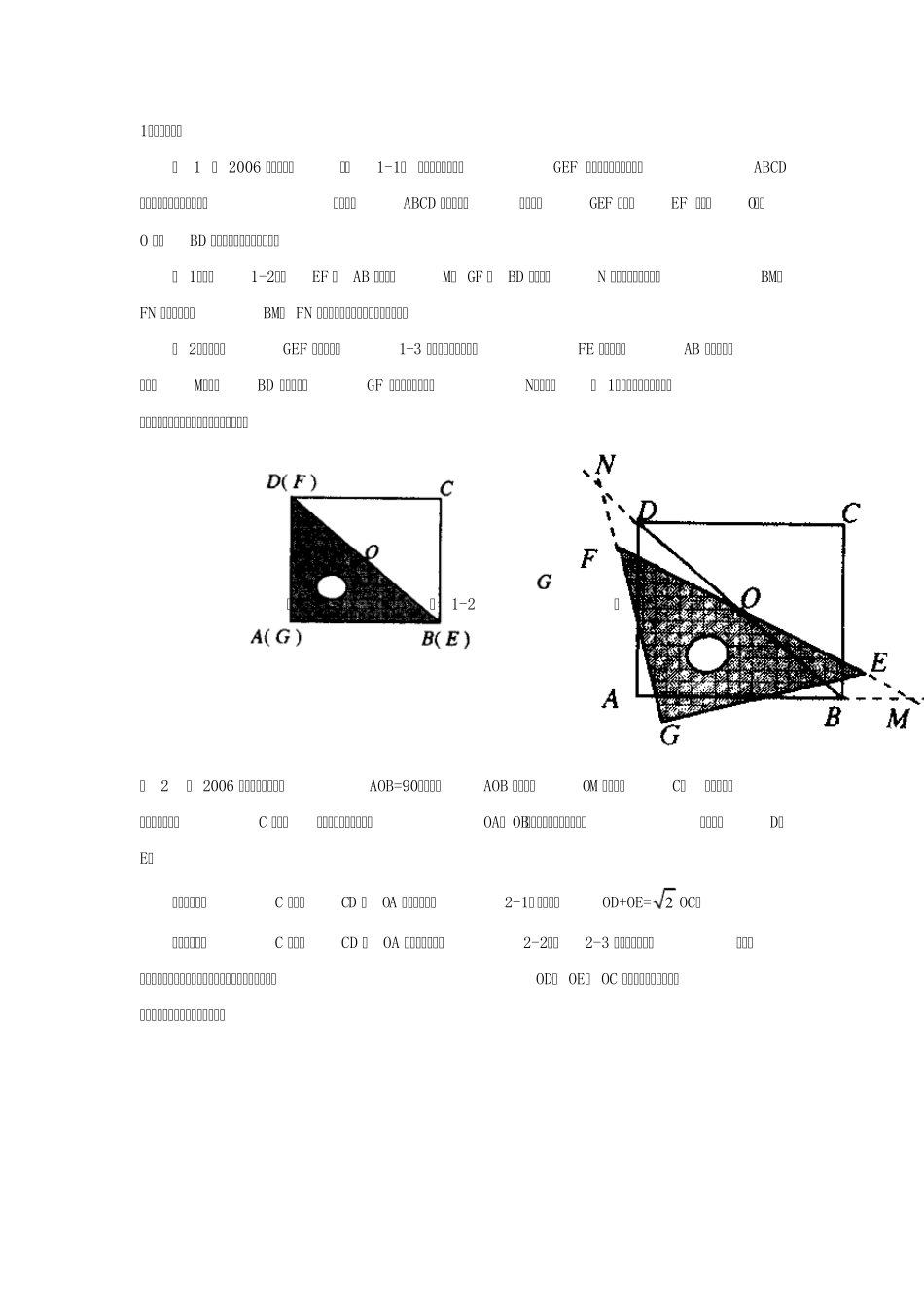
1.一块三角形 例1 ( 2006 年河北省)如图1-1, •一等腰直角三角尺GEF•的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF•的中点O(点O 也是BD 中点)按顺时针方向旋转. ( 1)如图1-2,当EF 与AB 相交于点M, GF 与BD 相交于点N 时,通过观察或测量BM,FN 的长度,猜想BM, FN 满足的数量关系,并证明你的猜想: ( 2)若三角尺GEF 旋转到如图1-3 所示的位置时,线段FE 的延长线与AB 的延长线相交于点M,线段BD 的延长线与GF 的延长线相交于点N,此时,( 1)中的猜想还成立吗?•若成立,请证明;若不成立,请说明理由. 图1-1 图1-2 图1-3 例2 ( 2006 年鸡西市)已知∠AOB=90°,在∠AOB 的平分线OM 上有一点C, •将一个三角板的直角顶点与C 重合,它的两条直角边分别与OA、 OB(或它们的反向延长线)相交于点D、E. 当三角板绕点C 旋转到CD 与OA 垂直时(如图2-1) ,易证:OD+OE=2 OC. 当三角板绕点C 旋转到CD 与OA 不垂直时,在图2-2、图2-3 这两种情况下,•上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、 OE、 OC 之间又有怎样的数量关系?请写出你的猜想,不需证明. 图2-1 图2-2 图2-3 3、旋转三角板 例6 如图6,三角板ABC 中,AC=b,∠C=90 °,将三角板ABC 饶C 点顺时针旋转90°,那么点A 移动所经过的路线是 。 (不取近似值) 2.二块三角板 2. 1 翻折、平移、旋转 1、 用三角板拼多边形 例1 用两块完全重合的等腰直角三角板,拼成下列图形: ①平行四边形(一般平行四边形)②矩形(不包含正方形)③正方形④等边三角形⑤等腰直角三角形,一定能拼成的图形是: : A)①②③ B)①③⑤ C)②③⑤ D)①③④⑤ 例2 用含30°的两个直角三角板,能拼成不同形状的平行四边形的个数为 : A) 1 个 B) 2 个 C) 3 个 D) 4 个 例4 用一副三角板可以拼成小于平角的角 个。 7、如图2,将一副直角三角板叠在一起,使直角顶点重合于点O,则 ∠ AOB+∠ DOC= 。 例5 把一副三角板的直角顶点O 重叠在一起, 1)如图4,当OB 平分∠COD 时,则∠AOD 和∠BOC 的和是多少度? 2)如图5,当OB 不平分∠COD 时,则∠AOD 和∠BOC 的和是多少度? 例3 ( 2006 年益阳市)如 图3,桌面内,直线L•上摆放着两块大小相同的直角三角板,它们中较小直角边...