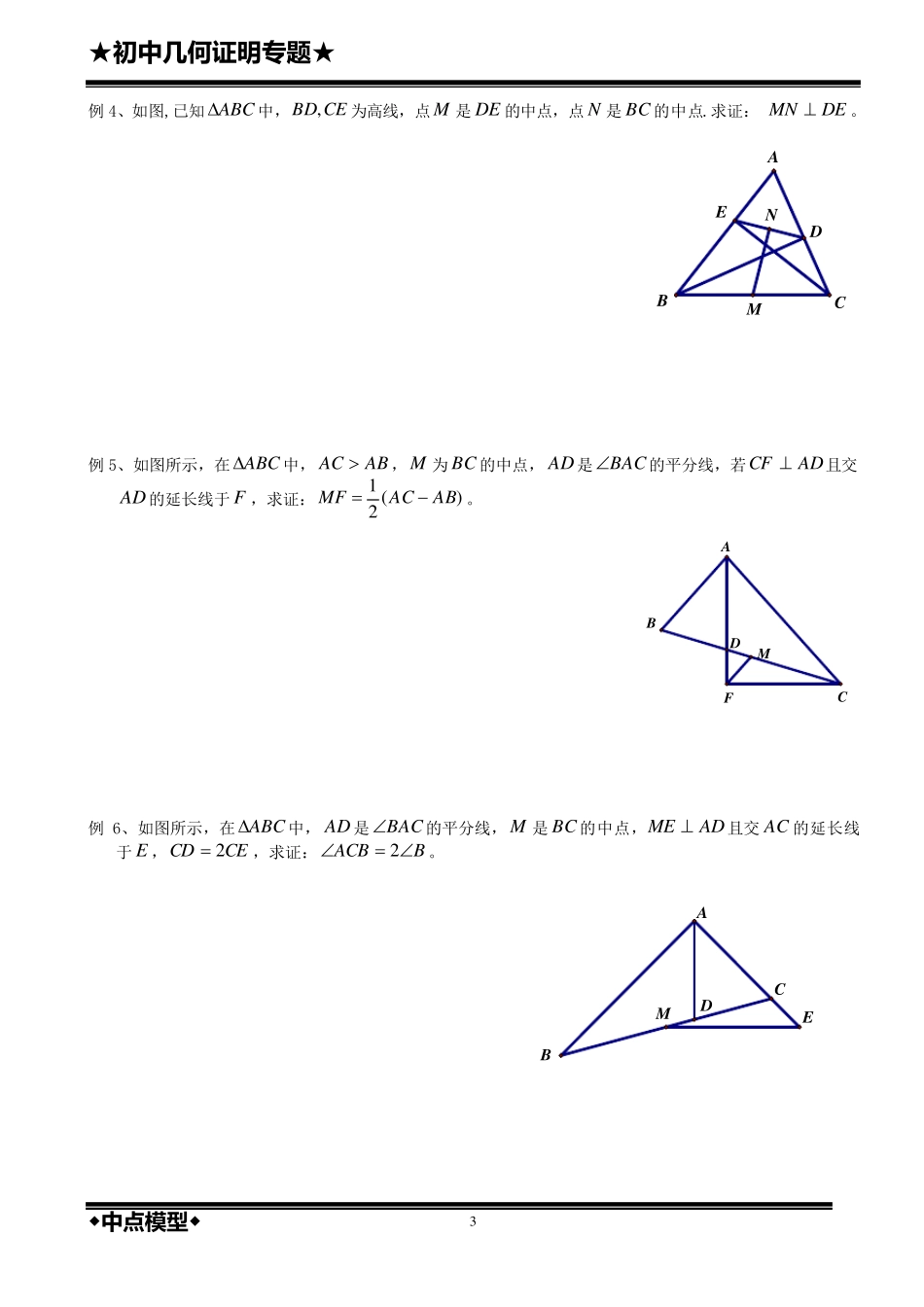
★初 中 几 何 证 明 专 题 ★ ◆中 点 模 型 ◆ 1 几 何 证 明 ——中 点 模 型 (中 级 ) 【知识要点 】 1、中位线定理:如图,在ABC中,若ADBD,AECE,则/ /DEBC 且12DEBC。 EDABC 2、中线倍长(倍长中线): 如图(左图),在ABC中,D 为BC 中点,延长AD 到E 使ADDE,连接BE ,则有:ADC≌EDB。 作用:转移线段和角。 ABCED DMCBA 注意: ①在实际运用中,与某个中点相连的线段,都可以将其看作“中线”,从而都可以考虑将它倍长(需要的话)。 ②如上右图,如果出现“两条平行线夹中点”的情形,一定会出现“X 全等”或“叉叉全等”或“8 字型全等”, 有时这个“叉叉”需要我们自己画出来(辅助线). 3、直角三角形斜边中线定理: 如图,在Rt ABC中,9 0ACB ,D 为AB 中点,则有:12CDADBDAB。 CBAD 4、三线合一: 在ABC中:(1)ACBC;(2)CD 平分ACB;(3)ADBD,(4)CDAB. “知二得二”:比如由(2)(3)可得出(1)(4).也就是说,以上四条语句,任意选择两个作为条件,就可以推出剩下两条。 DABC 请牢记:当你发现有某一条线同时具备了“垂线”、“角平分线”、“中线”三种功能当中的任意两种功能时,那么这条线就一定是某个等腰三角形的对称轴,换句话说,以这条线为对称轴必定有等腰三角形出现. ★初 中 几 何 证 明 专 题 ★ ◆中 点 模 型 ◆ 2 【经典例题 】 例 1、如图所示,已知 D 为 BC 中点,点 A 在 DE 上,且CEAB ,求证:CEDBAD. ADBCE 例 2、如图,已知在 ABC中, AD 是 BC 边上的中线,E 是 AD 上一点,且ACBE ,延长 BE 交 AC 于F ,求证:EFAF 。 FEDBCA 例 3、如图,在 ABC中, AD 为A的平分线, M 为 BC 的中点,M EAD//, 求证:ACABCFBE21。 FEDMBCA ★初 中 几 何 证 明 专题 ★ ◆中 点 模 型 ◆ 3 例 4、如图,已知 ABC中,CEBD,为高线,点 M 是 DE 的中点,点 N是 BC 的中点.求证: DEMN 。 NMDEBCA 例 5、如图所示,在 ABC中,ABAC ,M 为 BC 的中点, AD 是BAC的平分线,若ADCF 且交AD 的延长线于 F ,求证:)(21ABACMF。 DMAFCB 例 6、如图所示,在 ABC中, AD 是BAC的平分线, M 是 BC 的中点,ADME 且交 AC 的延长线于 E...