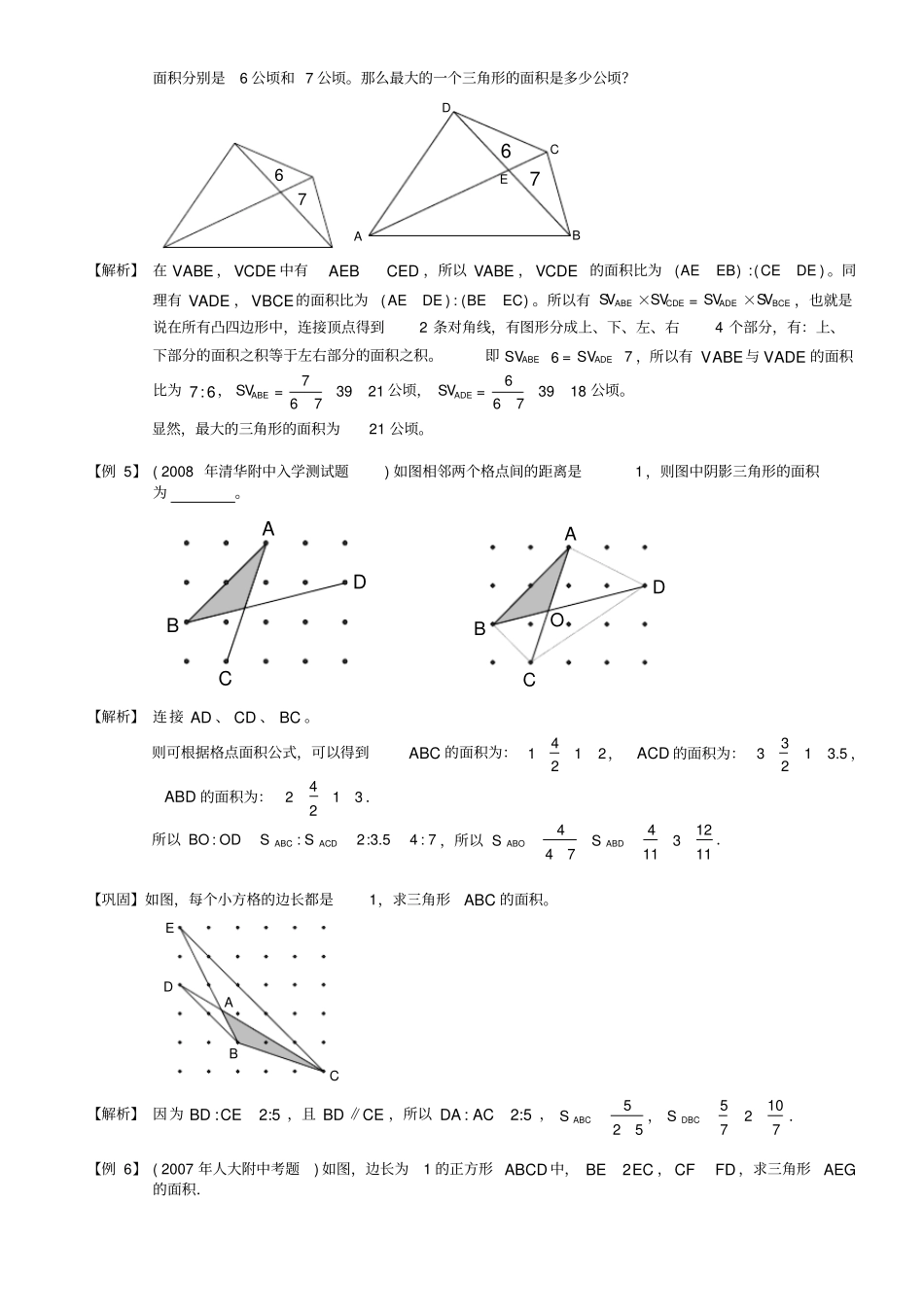
模型三蝴蝶模型 (任意四边形模型)任意四边形中的比例关系( “蝴蝶定理” ) :S4S3S2S1ODCBA①1243::SSSS 或者1324SSSS②1243::AO OCSSSS蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。【例 1】 ( 小数报竞赛活动试题) 如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分,△AOB面积为 1 平方千米, △BOC面积为 2 平方千米 ,△ COD的面积为3 平方千米,公园由陆地面积是6.92 平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得3 121.5AODS△平方千米,公园四边形ABCD 的面积是 1231.57.5平方千米,所以人工湖的面积是7.56.920.58平方千米【巩固】如图,四边形被两条对角线分成4 个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC?ABCDG321【解析】 ⑴根据蝴蝶定理,123BGCSV,那么6BGCSV;⑵根据蝴蝶定理,:12 : 361: 3AG GC. (??? )任意四边形、 梯形与相似模型【例 2】 四边形 ABCD 的对角线 AC 与 BD 交于点 O ( 如图所示 )。如果三角形ABD 的面积等于三角形BCD 的面积的 13,且2AO,3DO,那么 CO的长度是 DO 的长度的 _________倍。ABCDOHGABCDO【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。看到题目中给出条件:1:3ABDBCDSSVV,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形” ,于是可以作AH 垂直 BD 于 H , CG 垂直 BD 于 G ,面积比转化为高之比。再应用结论:三角形高相同,则面积之比等于底边之比,得出结果。请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题。解法一: ::1:3ABDBDCAO OCSS,∴236OC,∴:6:32:1OC OD.解法二:作AHBD 于 H , CGBD 于 G . 13ABDBCDSS,∴13AHCG ,∴13AODDOCSS,∴13AOCO ,∴236OC,∴:6:32:1OC OD.【例 3】 如图,平行四边形ABCD 的对角线交于O 点,CEF△、OE...