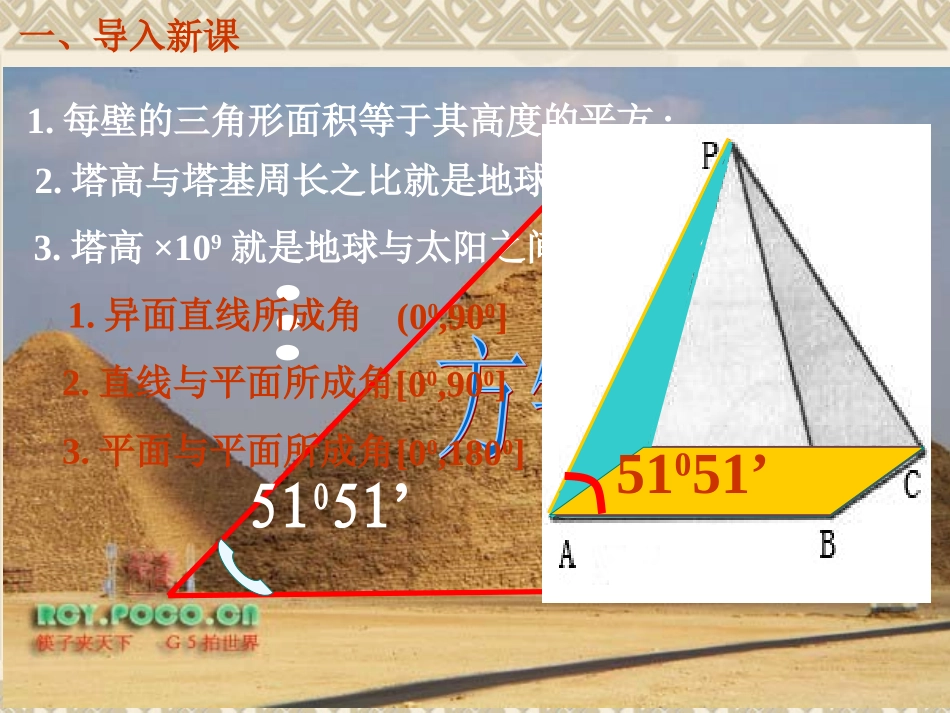
●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏1“几何法”解空间角宁波大红鹰职业技术学校章民●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏2一、导入新课1.每壁的三角形面积等于其高度的平方;2.塔高与塔基周长之比就是地球半径与周长之比;3.塔高×109就是地球与太阳之间的距离;51051’1.异面直线所成角2.直线与平面所成角3.平面与平面所成角(00,900][00,900][00,1800]51051’●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏3例1:有一位数学爱好者爬上了一座金字塔进行研究。测得:这座金字塔的底面边长和侧棱长都为2(百米)。他想知道:1)侧棱与相对底边所成的角。2)侧棱与底面所成的角。3)侧面与底面所成的角。三、方法归纳求:1)直线PA与CD所成角;2)直线PA与平面ABCD所成角;3)平面PAD与平面ABCD所成角的余弦值。●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏4任务:1.解出相应的题目;2.归纳你的解题思想和步骤;●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏51)直线PA与CD的所成角;2)直线PA与平面ABCD所成角;3)平面PAD与平面ABCD所成角的余弦值。oE∠PAB∠PEO∠PAO●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏6三、方法归纳:异面直线所成角:平移—说明所找的角—构造可解三角形求角平面与平面所成二面角:找平面角—说明所找的角—构造可解三角形求角归纳“几何法”解题步骤:一找,几何法直线与平面所成角:找射影—说明所找的角—构造可解三角形求角二证,三求.●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏7例2:当一位男数学爱好者沿着侧棱CP爬上一座金字塔进行研究。爬到一半时,他想研究:四、层次训练●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏81)两直线DE与AB所成的角2)直线DE与平面ABCD所成角的正弦值3)平面DEB与平面DBC所成的角●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏91)两直线DE与AB所成的角DCE●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏102)直线DE与平面ABCD所成角正弦值oGDGE●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏11o3)平面DEB与平面DBC所成的角OCE●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏12例3:当一位女数学爱好者沿着BP往上爬,到达中点F处.问:(1)男和A点的连线EA与底面所成的角,女和A点的连线FA与底面所成的角,比较两角大小?(利用角的正切值判断)(2)如果要使两角相等,哪一方还要爬多高?五、拓展训练男女F(男)(女)●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏13FoQHAHQAQE●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏14男女F●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏15六、小结提高:一、化归思想:空间角平面角构建三角形求内角二、“几何法”的解题步骤:一找,二证,三求。三、学习了这堂课后,对你以后的学习有何启发?●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏16必做题:1.矩形ABCD中,AB=4,BC=2,PA⊥平面ABCD,且PA=4,O为对角线交点,点M为PA的中点。求:1)直线PC与直线BD所成的角;2)直线PC与平面ABCD所成的角;3)平面MBD与平面ABCD所成的角。2.在长方体ABCD-A1B1C1D1中,已知AB=2,AD=,AA1=2,E为底面对角线交点。求:1)直线CD1与AB所成的角;2)D1E与底面ABCD所成的角;3)截面ACD1与底面ABCD所成的角。55七、分层落实●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏17选做题:3.四棱锥P-ABCD的底面是边长为1的正方形,PD⊥面ABCD,PB=3。求:(1)求直线AB与PC所成角的大小;(2)求PD与面PAB所成角的大小;(3)面PAD与面PBC所成的角。4.探究题:例3。●▂●书山有路勤为径学海无涯苦作舟专业分享,敬请收藏18