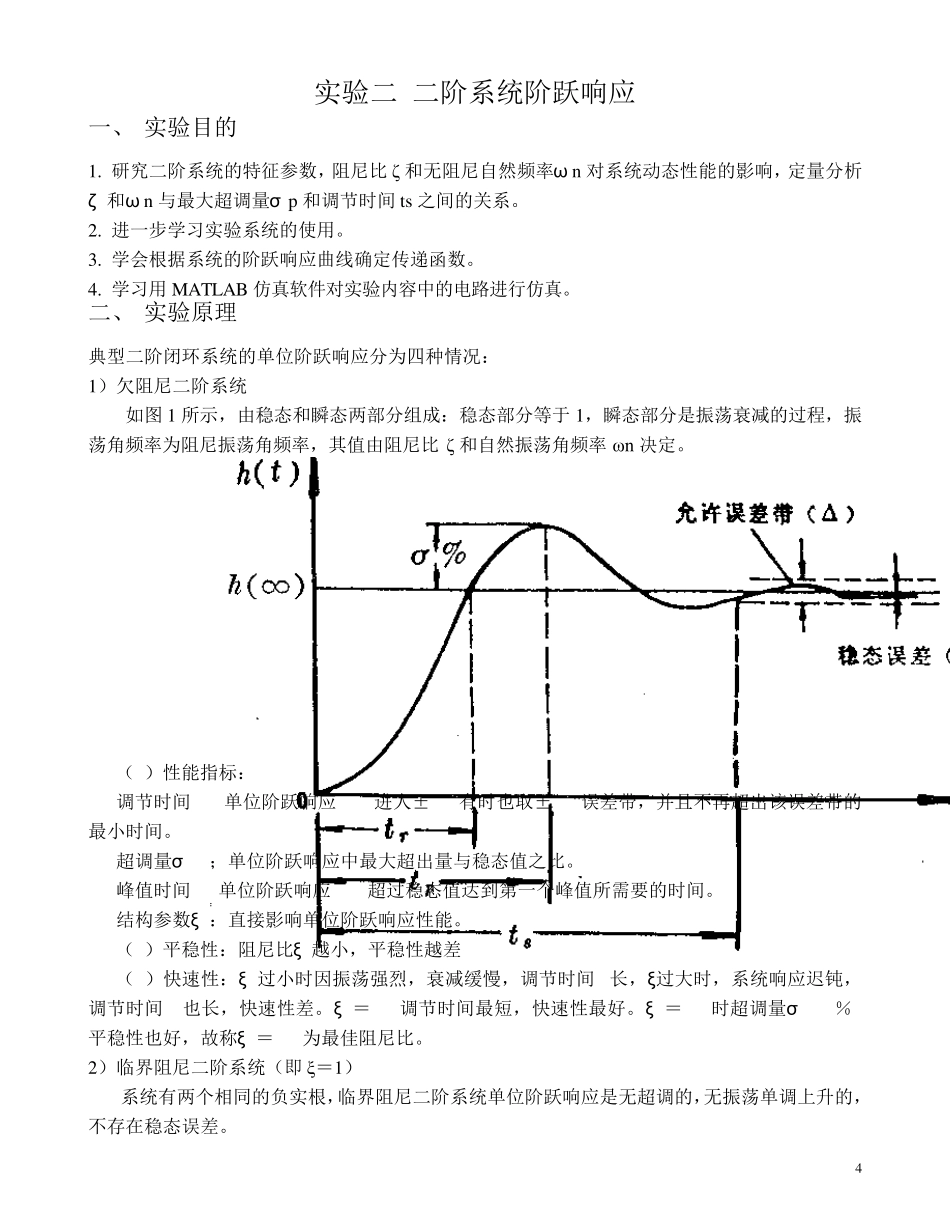
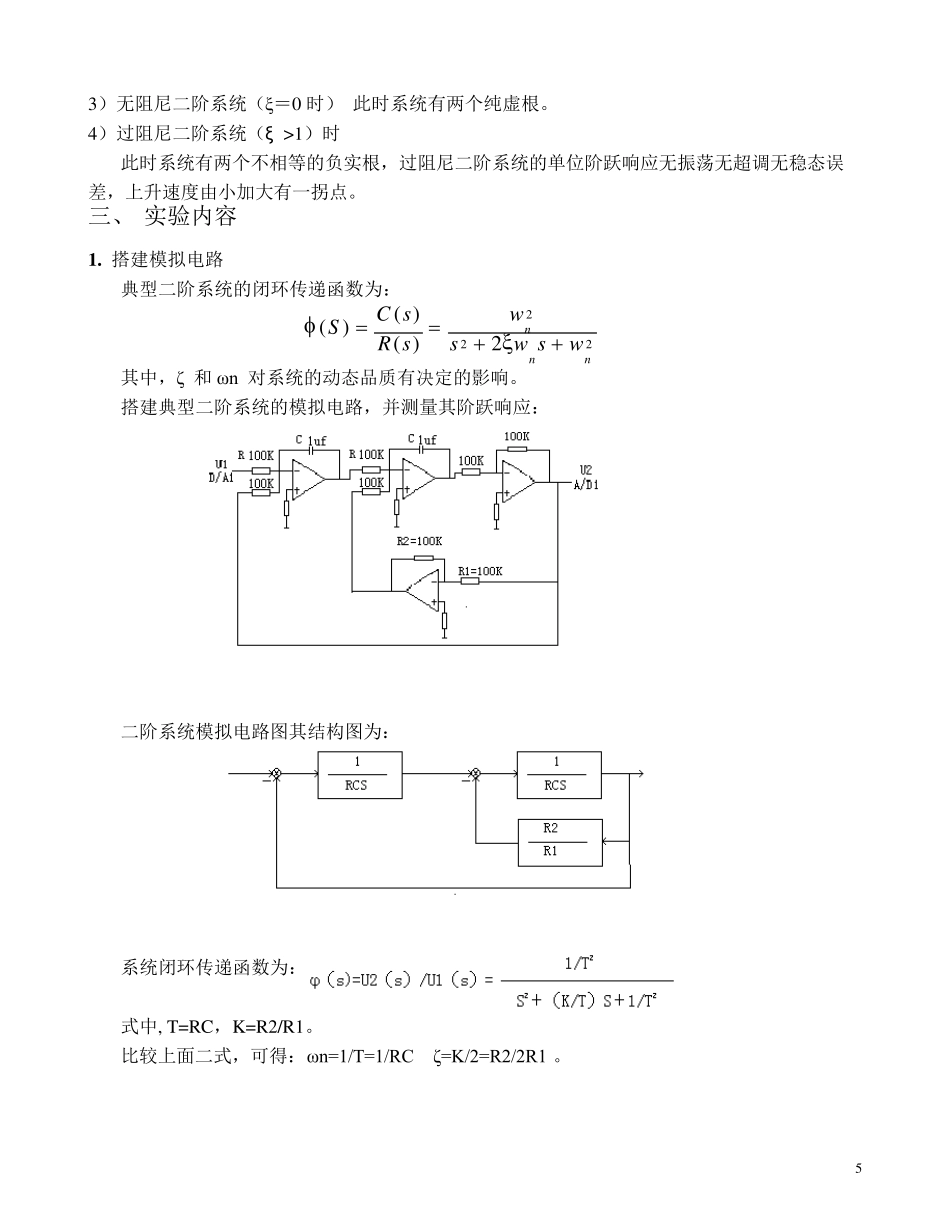
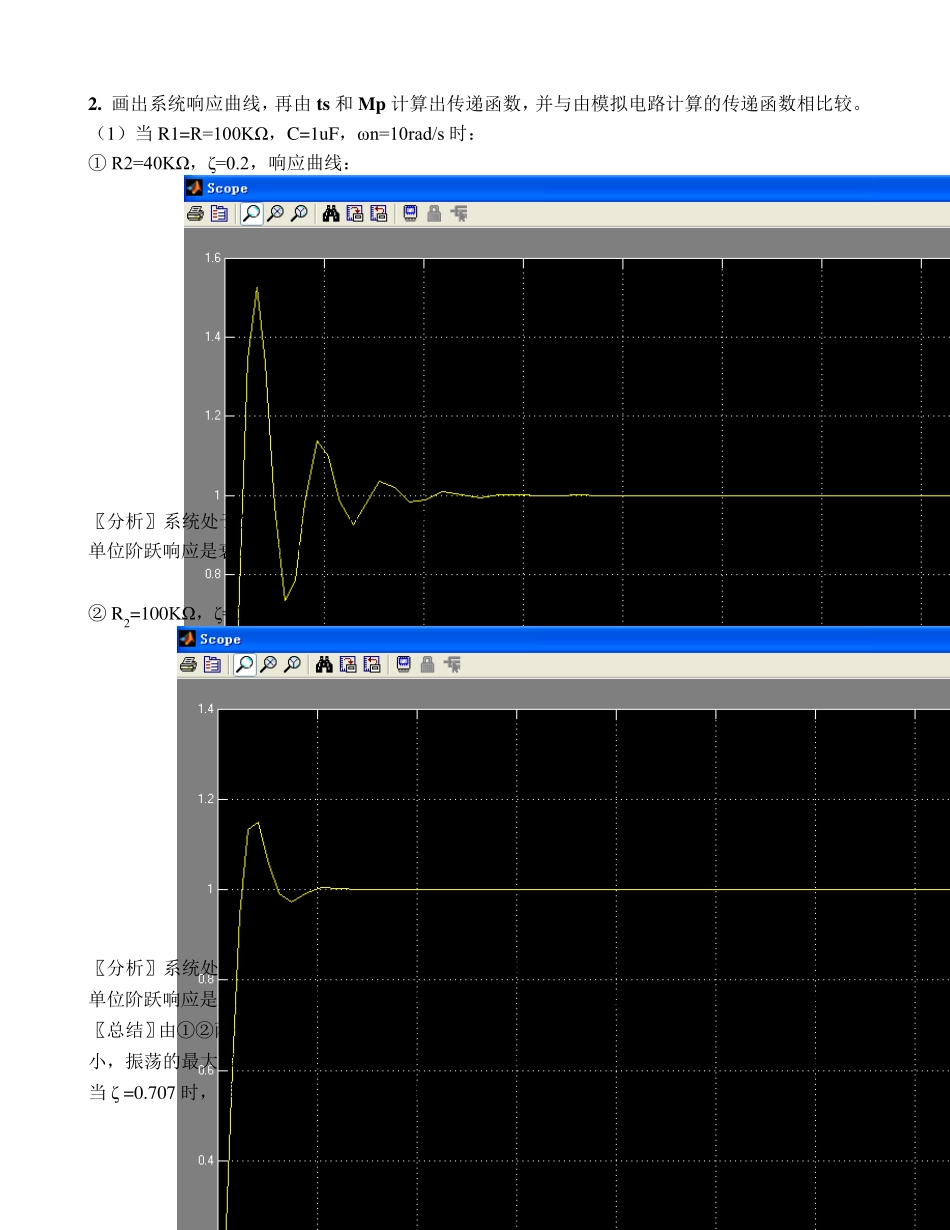
4 实验二 二阶系统阶跃响应 一、 实验目的 1. 研究二阶系统的特征参数,阻尼比ζ 和无阻尼自然频率ω n 对系统动态性能的影响,定量分析ζ 和ω n 与最大超调量σ p 和调节时间ts 之间的关系。 2. 进一步学习实验系统的使用。 3. 学会根据系统的阶跃响应曲线确定传递函数。 4. 学习用MATLAB 仿真软件对实验内容中的电路进行仿真。 二、 实验原理 典型二阶闭环系统的单位阶跃响应分为四种情况: 1)欠阻尼二阶系统 如图1 所示,由稳态和瞬态两部分组成:稳态部分等于1,瞬态部分是振荡衰减的过程,振荡角频率为阻尼振荡角频率,其值由阻尼比ζ 和自然振荡角频率ωn 决定。 (1)性能指标: 调节时间tS: 单位阶跃响应C(t)进人±5%(有时也取±2%)误差带,并且不再超出该误差带的最小时间。 超调量σ % ;单位阶跃响应中最大超出量与稳态值之比。 峰值时间tP :单位阶跃响应C(t)超过稳态值达到第一个峰值所需要的时间。 结构参数ξ :直接影响单位阶跃响应性能。 (2)平稳性:阻尼比ξ 越小,平稳性越差 (3)快速性:ξ 过小时因振荡强烈,衰减缓慢,调节时间tS长,ξ过大时,系统响应迟钝,调节时间tS 也长,快速性差。ξ =0.7调节时间最短,快速性最好。ξ =0.7时超调量σ %<5%,平稳性也好,故称ξ =0.7为最佳阻尼比。 2)临界阻尼二阶系统(即 ξ=1) 系统有两个相同的负实根,临界阻尼二阶系统单位阶跃响应是无超调的,无振荡单调上升的,不存在稳态误差。 5 3)无阻尼二阶系统(ξ=0 时) 此时系统有两个纯虚根。 4)过阻尼二阶系统(ξ >1)时 此时系统有两个不相等的负实根,过阻尼二阶系统的单位阶跃响应无振荡无超调无稳态误差,上升速度由小加大有一拐点。 三、 实验内容 1 . 搭建模拟电路 典型二阶系统的闭环传递函数为: 其中,ζ 和 ω n 对系统的动态品质有决定的影响。 搭建典型二阶系统的模拟电路,并测量其阶跃响应: 二阶系统模拟电路图其结构图为: 系统闭环传递函数为: 式中, T=RC,K=R2/R1。 比较上面二式,可得:ω n=1/T=1/RC ζ=K/2=R2/2R1 。 2222)()()(nnnwswswsRsCS 6 2. 画出系统响应曲线,再由ts 和Mp 计算出传递函数,并与由模拟电路计算的传递函数相比较。 (1)当R1=R=100KΩ,C=1uF,ωn=10rad/s 时: ① R2=40KΩ,ζ=0.2,响应曲线: 〖分析〗系统处于欠阻尼状态,0<ζ<1。系统的闭环根为两个共...