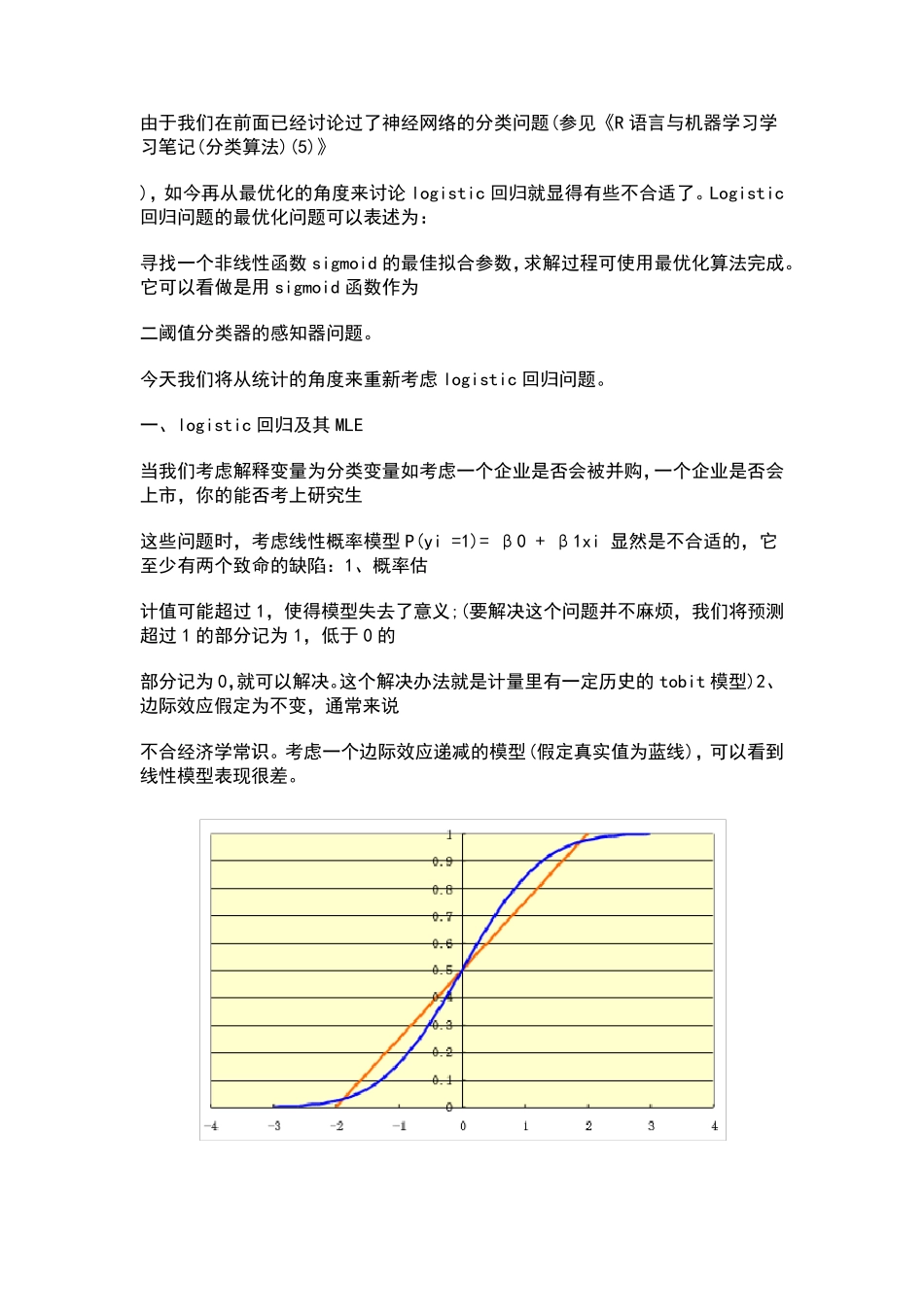
写在前面的废话 2014,又到了新的一年,首先祝大家新年快乐,也感谢那些关注我的博客的人。 现在想想数据挖掘课程都是去年的事了,一直预告着,盘算着年内完工的分类算法也拖了一年了。 本来打算去年就完成分类算法,如果有人看的话也顺带提提关联分析,聚类神马的, 可是,。 借着新年新气象的借口来补完这一系列的文章, 可是,这明明就是在发。 尽管这个是预告里的最后一篇,但是我也没打算把这个分类算法就这么完结。尽管每一篇都很浅显,每个算法 都是浅尝辄止的,在deep learning 那么火的今天,掌握这些东西算起来屌丝得不能再屌丝了。考虑到一致性 与完备性,最后补上两篇一样naive 的:组合方法提高分类效率、几种分类方法的绩效讨论。希望读到的人喜欢。 算法六:logistic 回归 由于我们在前面已经讨论过了神经网络的分类问题(参见《R 语言与机器学习学习笔记(分类算法)(5)》 ),如今再从最优化的角度来讨论logistic 回归就显得有些不合适了。Logistic回归问题的最优化问题可以表述为: 寻找一个非线性函数sigmoid 的最佳拟合参数,求解过程可使用最优化算法完成。它可以看做是用sigmoid 函数作为 二阈值分类器的感知器问题。 今天我们将从统计的角度来重新考虑logistic 回归问题。 一、logistic 回归及其MLE 当我们考虑解释变量为分类变量如考虑一个企业是否会被并购,一个企业是否会上市,你的能否考上研究生 这些问题时,考虑线性概率模型P(yi =1)= β0 + β1xi 显然是不合适的,它至少有两个致命的缺陷:1、概率估 计值可能超过1,使得模型失去了意义;(要解决这个问题并不麻烦,我们将预测超过1 的部分记为1,低于0 的 部分记为0,就可以解决。这个解决办法就是计量里有一定历史的tobit 模型)2、边际效应假定为不变,通 常 来说 不合经济 学常 识 。考虑一个边际效应递 减 的模型(假定真 实 值为蓝 线),可以看到线性模型表现 很 差 。 但是sigmoid 函数去拟合蓝线确实十分合适的。于是我们可以考虑logistic 回归模型: 假定有N 个观测样本Y1,Y2,…,YN,设P(Yi=1|Xi)=π(Xi)为给定条件 Xi 下得到结果 Yi=1 的条件概率;而在同 样条件下得到结果 Yi=0 的条件概率为 P(Yi=0|Xi)=1-π(Xi),于是得到一个观测值的概率 P(Yi)=π(Xi)Yi[1-π(Xi)] 1-Yi 假设各观测独立,对 logistic 回归模型来说,其对数似然函数为: 于是便可求解出 logistic 模型的MLE。 二、...