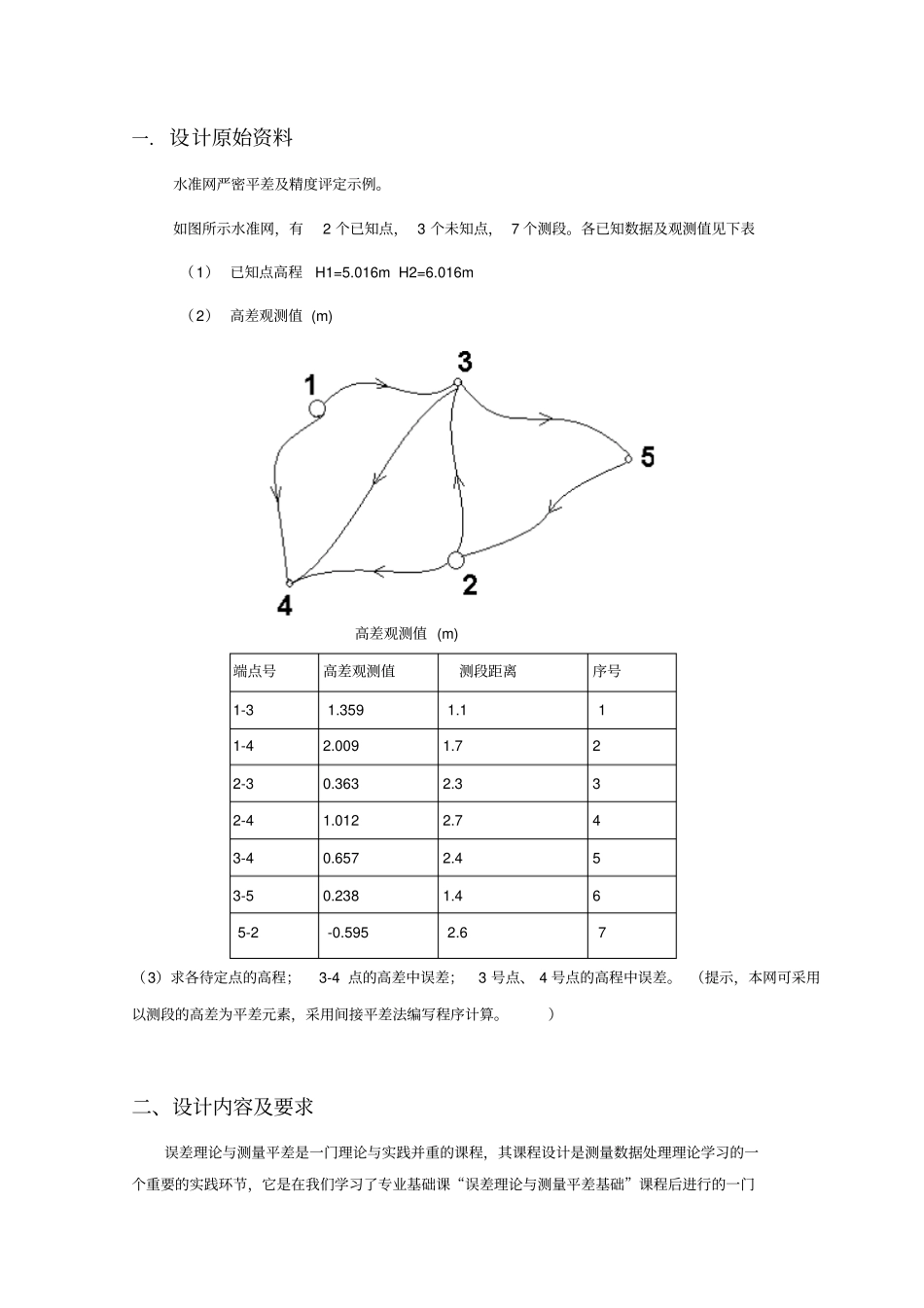
一.设计原始资料水准网严密平差及精度评定示例。如图所示水准网,有2 个已知点, 3 个未知点, 7 个测段。各已知数据及观测值见下表(1) 已知点高程H1=5.016m H2=6.016m (2) 高差观测值 (m) 高差观测值 (m) 端点号高差观测值测段距离序号1-3 1.359 1.1 1 1-4 2.009 1.7 2 2-3 0.363 2.3 3 2-4 1.012 2.7 4 3-4 0.657 2.4 5 3-5 0.238 1.4 6 5-2 -0.595 2.6 7 (3)求各待定点的高程;3-4 点的高差中误差;3 号点、 4 号点的高程中误差。 (提示,本网可采用以测段的高差为平差元素,采用间接平差法编写程序计算。)二、设计内容及要求误差理论与测量平差是一门理论与实践并重的课程,其课程设计是测量数据处理理论学习的一个重要的实践环节,它是在我们学习了专业基础课“误差理论与测量平差基础”课程后进行的一门实践课程。其目的是增强我们对误差理论与测量平差基础理论的理解,牢固掌握测量平差的基本原理和基本公式,熟悉测量数据处理的基本技能和计算方法,灵活准确地应用于解决各类数据处理的实际问题,正确应用条件平差模型列出观测值条件方程、误差方程、法方程和解算法方程,得出平差后的平差值及各待定点的高程平差值,评定各平差值的精度和各高程平差值的精度,并能用所学的计算机理论知识,编制简单的计算程序。三、水准网间接平差思路⑴.根据网型确定已知水准点数,未知水准点数u,总点数n, 总的观测高差段数 hn,必要观测数 t ,多余观测数r 。⑵. 确定参数。为平差后能直接求得待定点高程平差值,以 3 个待定点高程平差值为参数。设 3,4,5点的高程平差值分别为,,。⑶.列立条件方程. 左侧为观测值(系数为1),右侧为参数和常数项,并进一步改化成误差方程,最终写成矩阵形式。得到系数矩阵A 和常数项 L ⑷. 列立法方程,并解求法方程。由于该水准网间接平差误差方程个数为7 个而未知数个数为10 个,所列的误差方程是一组相容方程,有无数组解,所以必须在最小二乘原则(VTPV=min)的基础上利用拉格朗日乘数法求解. 令 F= VTPV-2KT(V-A+L), 分别对V 和求导,并令其导数为零,得到2VTP-2KT=0,ATK=0,将二式合并即得法方程:ATPV=ATPA-ATPL=0。求出 Naa= ATPA,W= ATPL,即得到相应的法方程。求解法方程,得到=N-1aaW加上 Xi 即可得到待定点的高程平差值,将代入误差方程得到相应的 V 值, hi+Vi得到各段高差的平差值。⑸.精度评定。计算单位权中...