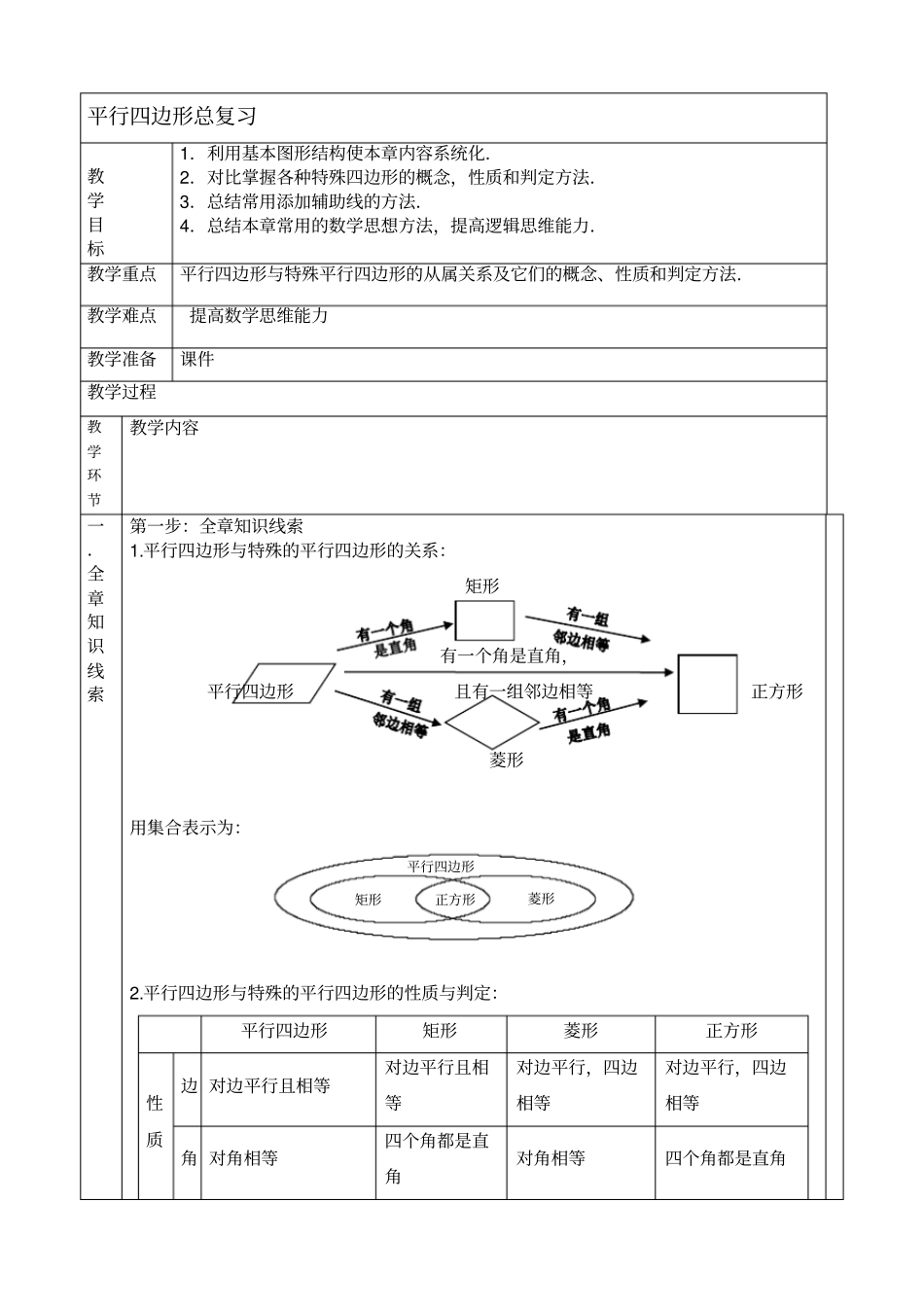
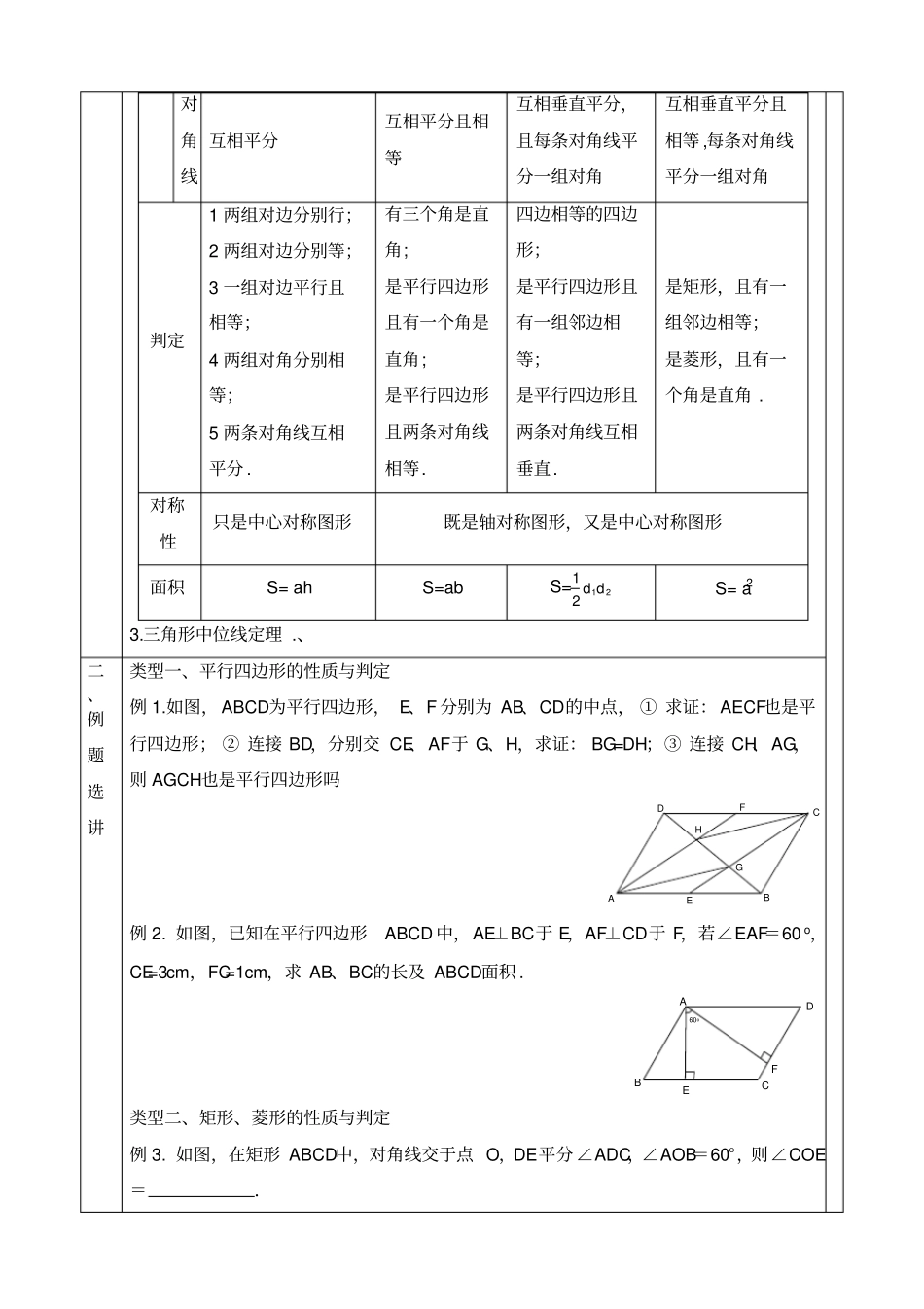
正方形菱形矩形平行四边形平行四边形总复习教学目标1.利用基本图形结构使本章内容系统化.2.对比掌握各种特殊四边形的概念,性质和判定方法.3.总结常用添加辅助线的方法.4.总结本章常用的数学思想方法,提高逻辑思维能力.教学重点平行四边形与特殊平行四边形的从属关系及它们的概念、性质和判定方法.教学难点提高数学思维能力教学准备课件教学过程教学环节教学内容一.全章知识线索第一步:全章知识线索1.平行四边形与特殊的平行四边形的关系:矩形有一个角是直角,平行四边形且有一组邻边相等正方形菱形用集合表示为:2.平行四边形与特殊的平行四边形的性质与判定:平行四边形矩形菱形正方形性质边 对边平行且相等对边平行且相等对边平行,四边相等对边平行,四边相等角 对角相等四个角都是直角对角相等四个角都是直角对角线互相平分互相平分且相等互相垂直平分,且每条对角线平分一组对角互相垂直平分且相等 ,每条对角线平分一组对角判定1 两组对边分别行;2 两组对边分别等;3 一组对边平行且相等;4 两组对角分别相等;5 两条对角线互相平分 .有三个角是直角;是平行四边形且有一个角是直角;是平行四边形且两条对角线相等.四边相等的四边形;是平行四边形且有一组邻边相等;是平行四边形且两条对角线互相垂直.是矩形,且有一组邻边相等;是菱形,且有一个角是直角 .对称性只是中心对称图形既是轴对称图形,又是中心对称图形面积S= ahS=abS=1212d dS= a23.三角形中位线定理 .、二、例题选讲类型一、平行四边形的性质与判定例 1.如图, ABCD为平行四边形, E、F 分别为 AB、CD的中点, ① 求证: AECF也是平行四边形; ② 连接 BD,分别交 CE、AF于 G、H,求证: BG=DH;③ 连接 CH、AG,则 AGCH也是平行四边形吗ABCDEFGH例 2. 如图,已知在平行四边形ABCD 中,AE⊥BC于 E,AF⊥CD于 F,若∠EAF=60 o,CE=3cm,FC=1cm,求 AB、BC的长及 ABCD面积 .60oABCDEF类型二、矩形、菱形的性质与判定例 3. 如图,在矩形 ABCD中,对角线交于点 O,DE平分 ∠ADC,∠AOB=60°,则∠COE=.ABCDEO例 4. 如图,矩形 ABCD中的长 AB=8 cm ,宽 AD=5cm ,沿过 BD的中点 O 的直线对折,使 B 与 D 点重合,求证: BEDF为菱形,并求折痕EF的长.OFEDCBA类型三、正方形的性质与判定例 6. 如图,已知 E、 F分别是正方形 ABCD的边 BC、CD上的点, AE、AF分别与对角线 BD 相交于 M、N...