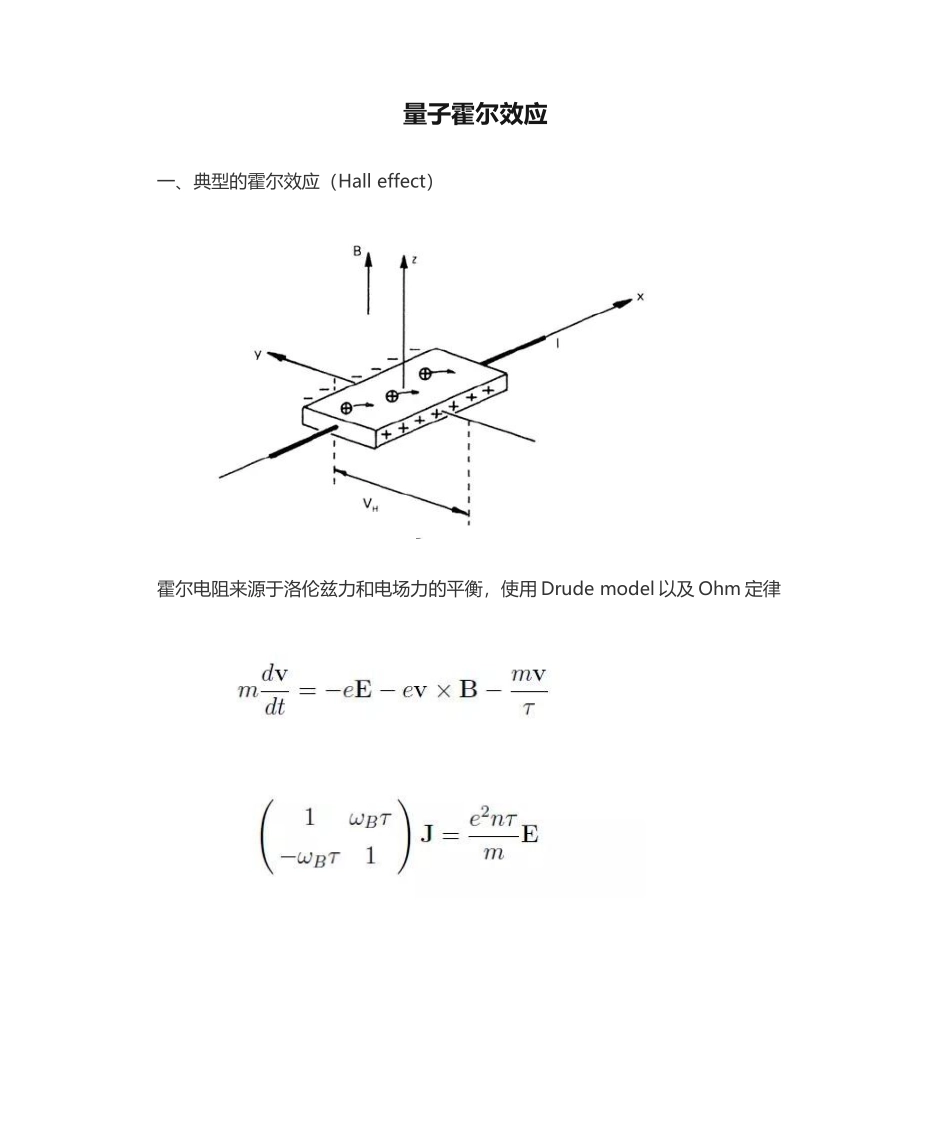
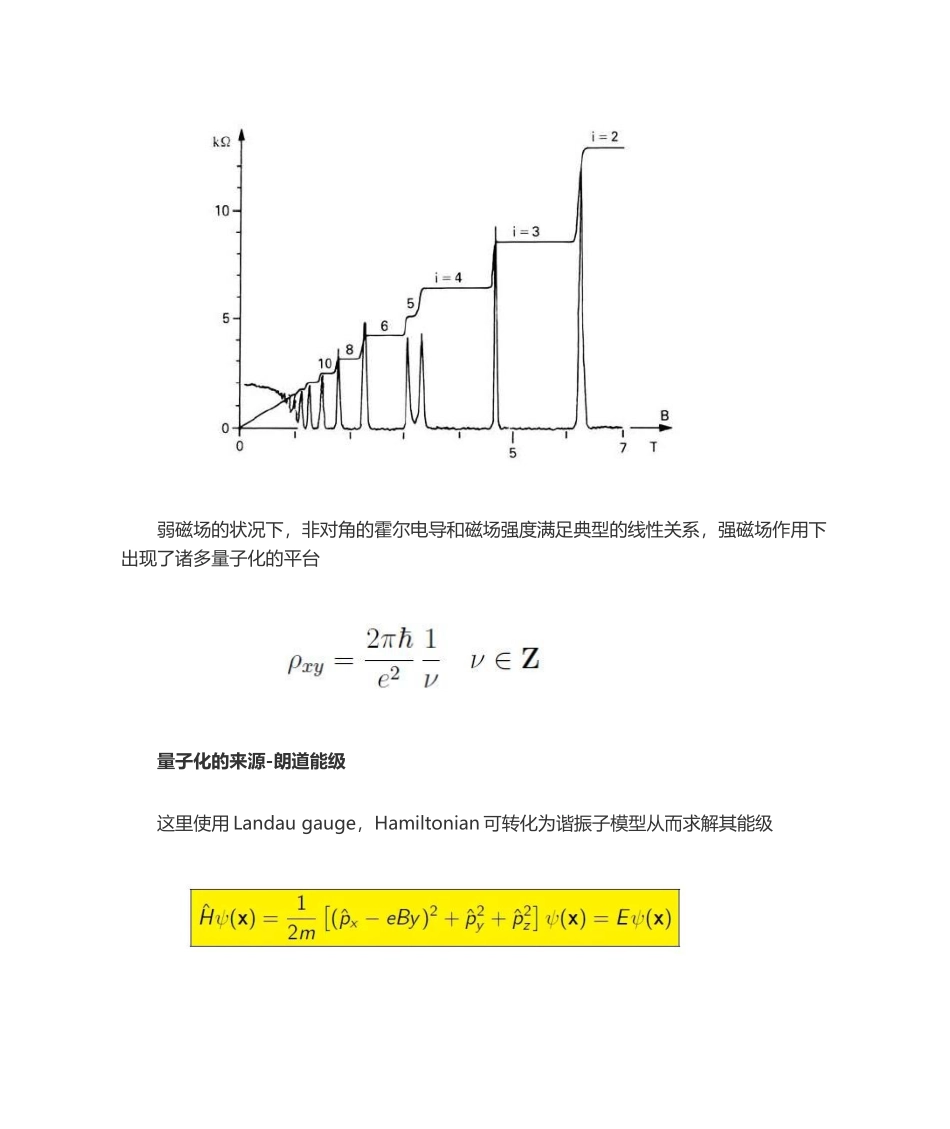
量子霍尔效应一、典型的霍尔效应(Hall effect)霍尔电阻来源于洛伦兹力和电场力的平衡,使用 Drude model 以及 Ohm 定律可得霍尔电导率(tensor)以及电阻率(tensor)二、(整数)量子霍尔效应弱磁场的状况下,非对角的霍尔电导和磁场强度满足典型的线性关系,强磁场作用下出现了诸多量子化的平台量子化的来源-朗道能级这里使用 Landau gauge,Hamiltonian 可转化为谐振子模型从而求解其能级波函数代入 current operator此时若在 y 方向加个电场 ε,破坏其对称性得到的 current 仍然是不变的(shift Gaussian wave packet center)。对电流积分可得量子化的霍尔电导率,其中 n 对应了朗道能级的占据数目Laughlin’s gauge argument将 IQHE 解释为 quantum pump,增加一种量子磁通的 test flux 的就对应着Gaussian wave packet 移动一种单位。Landauer's approach (Edge modes)Drift velocity 直接由化学电势差决定拓扑的引入 (Kubo Formula,Chern number or TKNN number,Berry curvature...)Kubo Formula 是通过 linear response 得到的电导率上式红色部分是纯虚数,Berry curvature 是纯实数因此第 n 个 band 的霍尔电导率是上式括号里面的积分是一种整数,即 Chern number (first Chern number)=TKNN number。证明略。。。复旦大学物理学系专家修发贤课题组通过对量子霍尔效应的研究,实现了从二维迈向三维的新突破。他们的科研成果于 12 月 18 日在线发表于《自然》期刊上。早在 1879 年,美国物理学家霍尔在研究金属的导电机制时发现,如果对通电的导体加上垂直于电流方向的磁场,电子的运动轨迹将发生偏转,在与导体纵向垂直的方向产生电压。这个电磁现象被称为“霍尔效应”,是 20 世纪以来凝聚态物理领域最重要的科学发现之一,迄今已有 4 个诺贝尔奖与其直接有关。然而 100 数年来,科学家们对量子霍尔效应的研究始终停留于二维体系,从未涉足三维领域。修发贤课题组近日在拓扑半金属砷化镉纳米片中观察到了由外尔轨道形成的新型三维量子霍尔效应的直接证据,从而迈出了从二维到三维的核心一步。如果将电子限制在二维平面内,在强大的磁场作用下,电子将能够在导体边沿做一维运动,就象是沿着房间的“天花板”或者“地面”的“边界限”在有条不紊地运动,一列朝前,一列向后,两列电子各行其道。那么,在立体空间中——三维体系中也存在量子霍尔效...