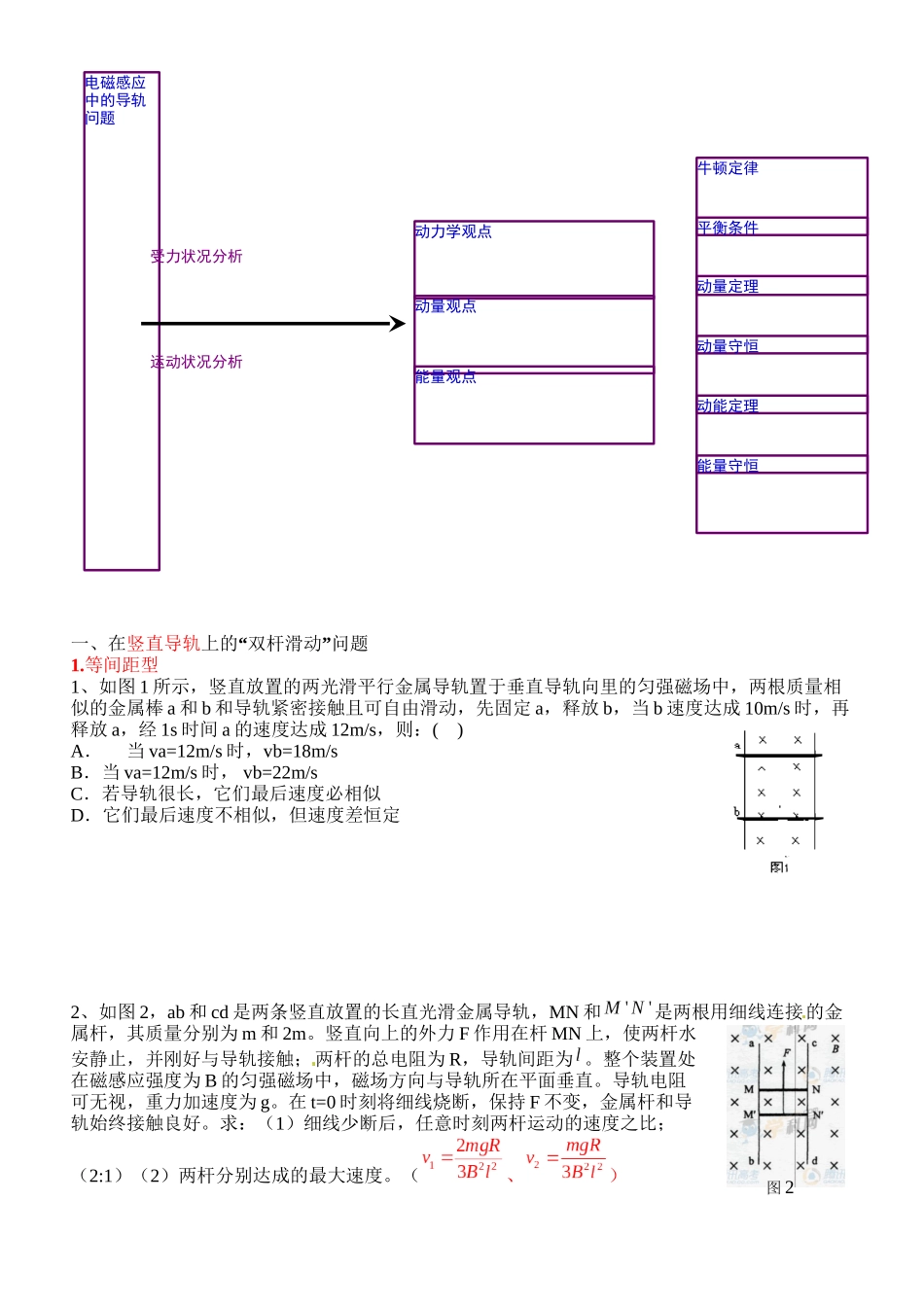
双 杆 切 割 磁 感 线 模 型 Prepared on 22 November 电磁感应中的导轨问题受力状况分析运动状况分析动力学观点动量观点能量观点牛顿定律平衡条件动量定理动量守恒动能定理能量守恒图 2一、在竖直导轨“”上的 双杆滑动 问题1.等间距型1、如图 1 所示,竖直放置的两光滑平行金属导轨置于垂直导轨向里的匀强磁场中,两根质量相似的金属棒 a 和 b 和导轨紧密接触且可自由滑动,先固定 a,释放 b,当 b 速度达成 10m/s 时,再释放 a,经 1s 时间 a 的速度达成 12m/s,则:( )A.当 va=12m/s 时,vb=18m/sB.当 va=12m/s 时, vb=22m/sC.若导轨很长,它们最后速度必相似D.它们最后速度不相似,但速度差恒定2、如图 2,ab 和 cd 是两条竖直放置的长直光滑金属导轨,MN 和是两根用细线连接的金属杆,其质量分别为 m 和 2m。竖直向上的外力 F 作用在杆 MN 上,使两杆水安静止,并刚好与导轨接触;两杆的总电阻为 R,导轨间距为 。整个装置处在磁感应强度为 B 的匀强磁场中,磁场方向与导轨所在平面垂直。导轨电阻可无视,重力加速度为 g。在 t=0 时刻将细线烧断,保持 F 不变,金属杆和导轨始终接触良好。求:(1)细线少断后,任意时刻两杆运动的速度之比;(2:1)(2)两杆分别达成的最大速度。(、)图 3图 42.不等间距型3、图中和为在同一竖直平面内的金属导轨,处在磁感应强度为 B 的匀强磁场中,磁场方向垂直导轨所在的平面(纸面)向里。导轨的段与段是竖直的.距离为小,段与段也是竖直的,距离为。与为两根用不可伸长的绝缘轻线相连的金属细杆,质量分别为和,它们都垂直于导轨并与导轨保持光滑接触。两杆与导轨构成的回路的总电阻为。F 为作用于金属杆上的竖直向上的恒力。已知两杆运动到图示位置时,已匀速向上运动,求此时作用于两杆的重力的功率的大小和回路电阻上的热功率。(; )二、在水平导轨“”上的 双杆滑动 问题(一)等间距水平导轨,无水平外力作用(安培力除外)4、够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为 l,导轨上面横放着两根导体棒 ab 和 cd,构成矩形回路,如图 4 所示,两根导体棒的质量皆为m,电阻皆为 R,回路中其它电阻不计,整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为 B,设两导体棒均可沿导轨无摩擦的滑行,开始时棒 cd 静止,棒 ab 有指向棒 cd 的初速度 v0, 若两导体棒在运动中始终不接触...