九、平面一般力系平衡方程的其他形式VIP免费

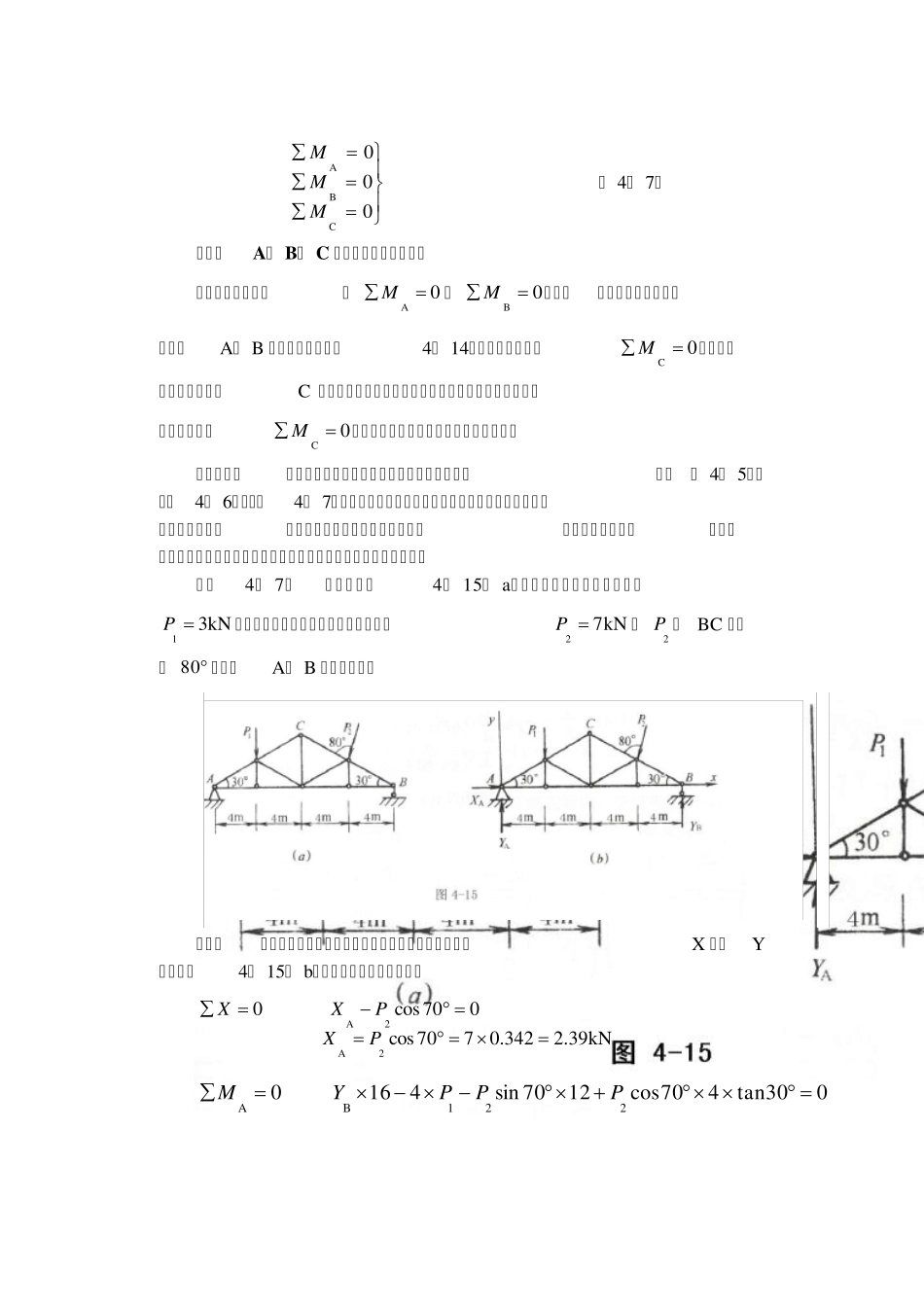
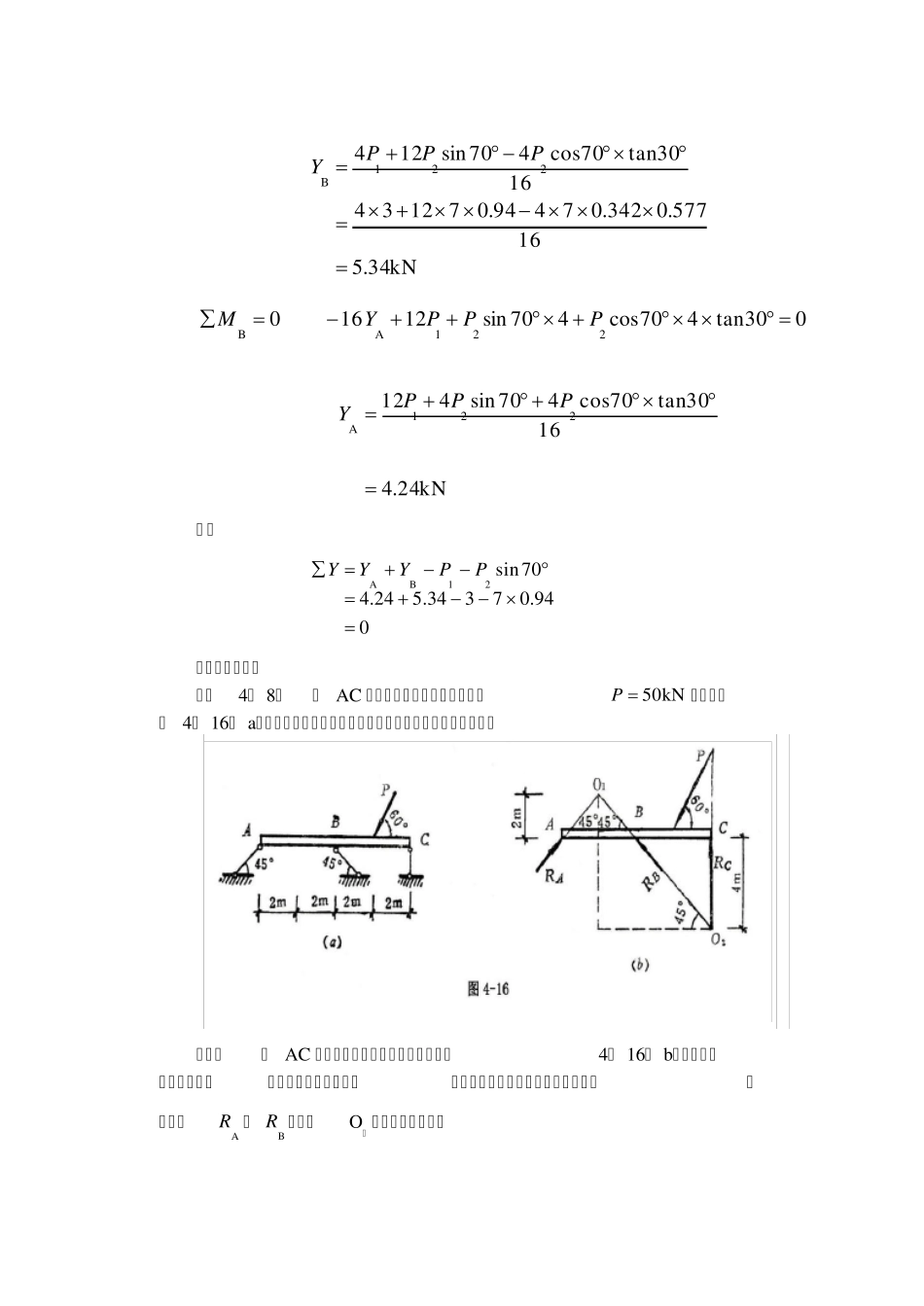
第九讲内容 一、平面一般力系平衡方程的其他形式 前面我们通过平面一般力系的平衡条件导出了平面一般力系平衡方程的基本形式，除了这种形式外，还可将平衡方程表示为二力矩形式及三力矩形式。 1．二力矩形式的平衡方程 在力系作用面内任取两点A、 B 及X 轴，如图4－ 13 所示，可以证明平面一般力系的平衡方程可改写成两个力矩方程和一个投影方程的形式，即 000BAMMX (4－ 6) 式中X 轴不与A、 B 两点的连线垂直。 证明：首先将平面一般力系向A 点简化，一般可得到过A 点的一个力和一个力偶。若0A M成立，则力系只能简化为通过A 点的合力R 或成平衡状态。如果0B  M又成立，说明R 必通过B。可见合力R 的作用线必为 AB 连线。又因0 X成立，则0XXR， 即合力R 在 X 轴上的投影为零，因AB 连线不垂直X 轴，合力R 亦不垂直于X 轴，由0X R可推得0R。可见满足方程（4－ 6）的平面一般力系，若将其向A 点简化，其主矩和主矢都等于零，从而力系必为平衡力系。 2．三力矩形式的平衡方程 在力系作用面内任意取三个不在一直线上的点A、 B、 C，如图4－ 14所示，则力系的平衡方程可写为三个力矩方程形式，即 000CBAMMM （ 4－ 7） 式中，A、 B、 C 三点不在同一直线上。 同上面讨论一样，若0A  M和0B  M成立，则力系合成结果只能是通过A、 B 两点的一个力（图4－ 14）或者平衡。如果0C  M也成立，则合力必然通过C 点，而一个力不可能同时通过不在一直线上的三点，除非合力为零，0C  M才能成立。因此，力系必然是平衡力系。 综上所述，平面一般力系共有三种不同形式的平衡方程，即式（ 4－ 5）、式（4－ 6）、式（4－ 7），在解题时可以根据具体情况选取某一种形式。无论采用哪种形式，都只能写出三个独立的平衡方程，求解三个未知数。任何第四个方程都不是独立的，但可以利用这个方程来校核计算的结果。 【例4－ 7】 某屋架如图4－ 15（ a）所示，设左屋架及盖瓦共重kN31 P，右屋架受到风力及荷载作用，其合力kN72 P，2P 与 BC 夹角为80 ，试求A、 B 支座的反力。 【解】 取整个屋架为研究对象，画其受力图，并选取坐标轴X 轴和Y轴，如图4－ 15（ b）所示，列出三个平衡方程 kN39.2342.0770cos 070cos 02A2APXPXX 030tan470cos1270sin416 0221BA...