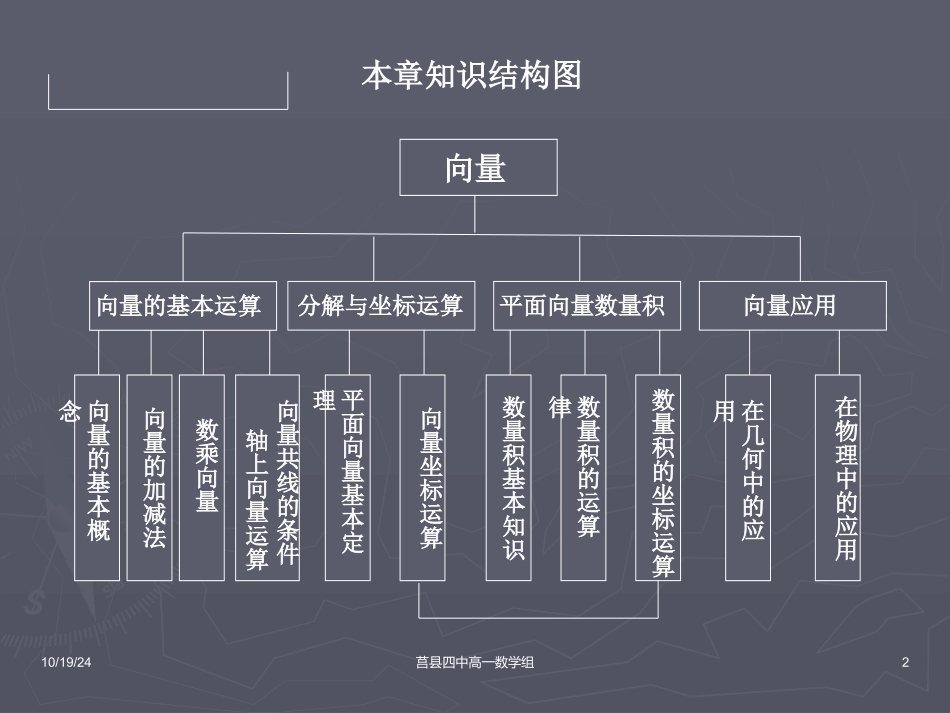
10/19/2410/19/24莒县四中高一数学组莒县四中高一数学组11向量的概念向量的概念10/19/24莒县四中高一数学组2本章知识结构图向量向量的基本运算分解与坐标运算平面向量数量积向量应用数量积的运算律数量积的坐标运算数量积基本知识在几何中的应用在物理中的应用向量的基本概念向量的加减法数乘向量向量共线的条件轴上向量运算平面向量基本定理向量坐标运算10/19/24莒县四中高一数学组3CAB老鼠由老鼠由AA处处向东向东以每秒以每秒66米的速度逃窜,米的速度逃窜,而猫由而猫由BB处处以每秒以每秒1010米米的速度追击的速度追击..若若BB处在处在AA处东处东88米,问猫能否抓米,问猫能否抓到老鼠?若能,如何在到老鼠?若能,如何在最短的时间内抓到老鼠?最短的时间内抓到老鼠?一千吨的棉花和一千吨的铁谁更重?一千吨的棉花和一千吨的铁谁更重?两个问题两个问题重量相等重量相等10/19/24莒县四中高一数学组4向量的概念与数量的区别既有大小又有方向的量叫向量.例:力、位移、加速度、速度等.数量与向量的区别:1.数量只有大小,是一个代数量,可以比较大小.2.向量有方向、大小,双重属性,而方向是不能比较大小的,因此向量不能比较大小.定义:注意:向量不能比较大小.10/19/24莒县四中高一数学组5(1)你能举出那些量是符合上述要求的量?(2)问题:温度是不是向量?重量呢?身高?海拔?速度?10/19/24莒县四中高一数学组6向量的表示向量的表示二、向量的表示方法1.几何法:用有向线段表示2.字母法:用小写字母表示注意:印刷体与手写的区别3.用表示向量的有向线段的起点和终点字母表示ABaa不是aAB�10/19/24莒县四中高一数学组71、向量的长度(模):向量的大小表示:AB||AB三、与向量有关的基本概念2、零向量与单位向量零向量:长度为零的向量(方向任意).表示:0|0|,0单位向量:长度为1个单位长度的向量.10/19/24莒县四中高一数学组833、向量之间的关系、向量之间的关系((11))平行向量:方向相同或相反的非零向量.表示:共线向量:任一组平行向量都可平移到同一直线上.即平行向量也叫做共线向量.特别的,零向量与任一向量平行.即:(2)相等向量:大小相等方向相同的向量表示:,与起点位置无关相反向量:大小相同方向相反的向量0//a//abab10/19/24莒县四中高一数学组9相等的向量PQL如图所示:一个向量平行移动后,所得向量与原向量相等.K※零向量和单位向量都是相等的10/19/24莒县四中高一数学组10思考1如图,表示平面上的六个平行四边形,问图中哪些向量分别与向量相等?那些向量与它们互为相反向量?ABADAE�、、ABCDEFGH10/19/24莒县四中高一数学组11►(1)(1)平行向量是否一定方向相反平行向量是否一定方向相反??►(2)(2)不相等向量是否一定不平行不相等向量是否一定不平行??►(3)(3)与零向量相等的向量是什么向量与零向量相等的向量是什么向量??►(4)(4)与任何向量都平行的向量是什么向量与任何向量都平行的向量是什么向量??►(5)(5)若两向量在同一直线上若两向量在同一直线上,,则它们是什么则它们是什么??►(6)(6)非零向量相等的充要条件是什么非零向量相等的充要条件是什么??►(7)(7)共线向量一定在一条直线上吗共线向量一定在一条直线上吗??10/19/24莒县四中高一数学组12例1.判断下列命题真假或给出问题的答案:(1)平行向量的方向一定相同.(2)不相等的向量一定不平行.(3)与零向量相等的向量是什么向量?(4)存在与任何向量都平行的向量吗?(5)若两个向量在同一直线上,则这两个向量一定是什么向量?(6)两个非零向量相等应满足什么条件?(7)共线向量一定在同一直线上.××零向量零向量平行向量(共线向量)模相等且方向相同×10/19/24莒县四中高一数学组13例例22下列情形中下列情形中,,向量终点构成什么向量终点构成什么图形图形??(1)(1)把所有单位向量移到同一个起点把所有单位向量移到同一个起点;;(2)(2)把平行于某一直线的所有单位向量平移到同把平行于某一直线的所有单位向量平移到同一起点一起点;;(3)(3)把平行于一直线的一切向量平移到同一起把平行于一直线的一切向量平移到同一起点点;;10/19/24莒县四中高一数学组14单击动画演示...