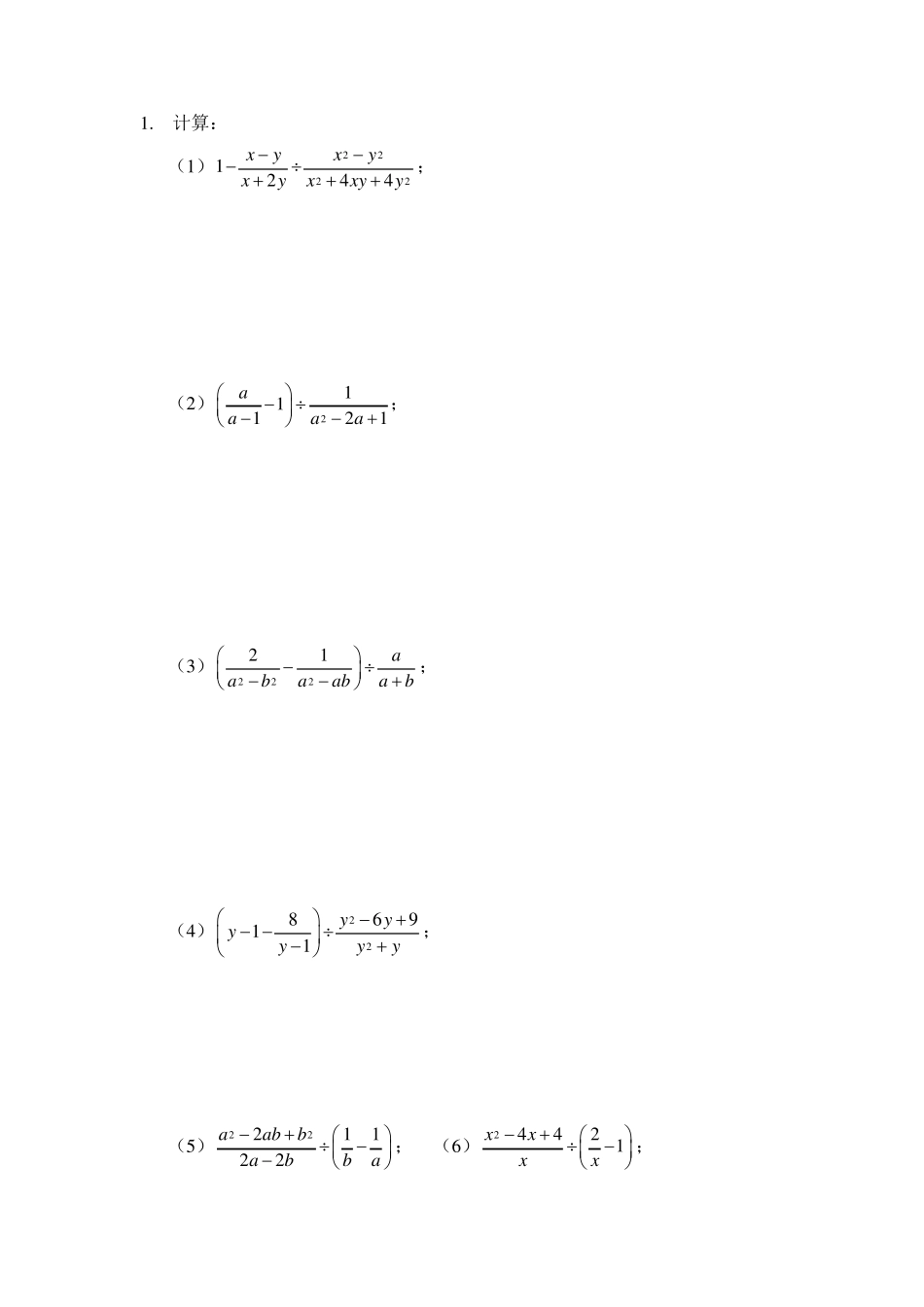分式混合运算(习题及答案)VIP免费

分式混合运算（习题） ➢ 例题示范 例1：混合运算：41 2222xxxx． 【过程书写】 22441 22241 622422 (4 )(4 )14xxxxxxxxxxxxxx    解：原式 例2：先化简(1)211x xxxxx，然后在22x ≤≤的范围内选取一个你认为合适的整数x 代入求值． 【过程书写】 2221122112xxxxxxxxxxxx 解：原式 22x ≤≤，且x 为整数 ∴使原式有意义的x 的值为-2，-1 或 2 当 x =2 时，原式=-2 ➢ 巩固练习 1 . 计算： （1 ）22221244xyxyxyxxyy； （2 ）211121aaaa； （3 ）22221aabaabab； （4 ）2286911yyyyyy ； （5 ）2221122aabbabba； （6 ）24421xxxx； （7 ）2234221121xxxxxx； （8 ） 352242xxxx； （9 ）253263xxxx； （1 0 ）211(1)111xxx； （11 ）22221113xyxyxyxxyxy ． 2 . 化简求值： （1 ）先化简，再求值：2121122xxxx，其中31x  ． （2 ）先化简，再求值：2222225321xyxxyyxx yxy，其中 32x ，32y ． （3 ）先化简22212211211xxxxxxxx，然后在22x ≤≤ 的范围内选取一个合适的整数 x 代入求值． （4）已知222111xxxAxx ． ①化简A； ②当x满足不等式组1030xx  ≥，且 x为整数时，求 A 的值． 3. 不改变分式2132113xyx的值，把分子、分母中各项系数化为整数，结果是（ ） A．263x yx B．218326xyx C．2331xyx D．218323xyx 4. 把分式32abab中的分子、分母的值同时扩大为原来的2 倍，则分式的值（ ） A．不变 B．扩大为原来的2 倍 C．扩大为原来的4 倍 D．缩小为原来的12 5. 把分式34abab中a，b 的值都扩大为原来的2 倍，则分式的值（ ） A．不变 B．扩大为原来的2 倍 C．扩大为原来的4 倍 D．缩小为原来的12 6. 把分式222xyxy中x，y 的值都...