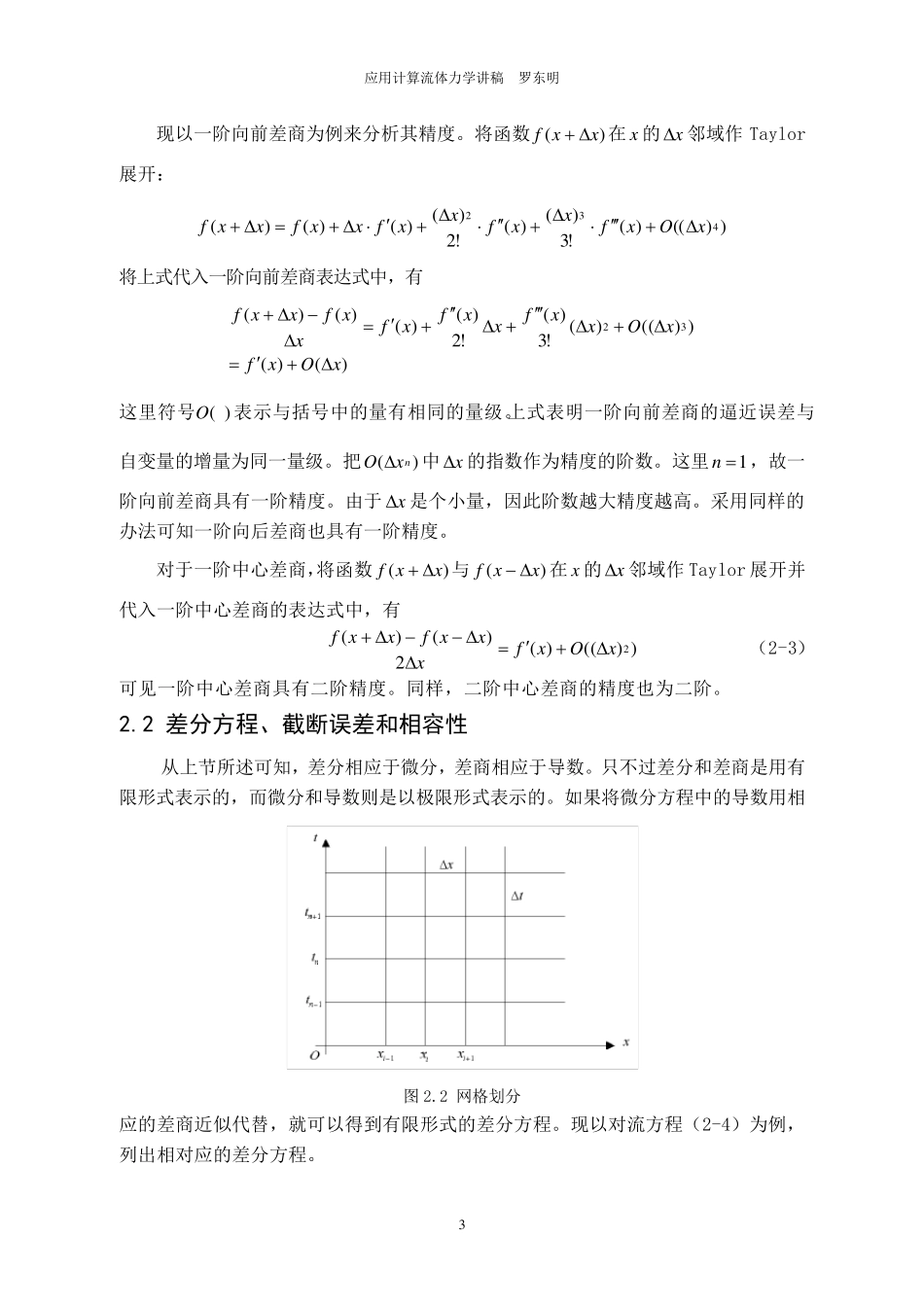
应用计算流体力学讲稿 罗东明 1 第二讲 有限差分法基本原理 一般的流体控制方程都是非线性的偏微分方程。在绝大多数情况下,这些偏微分方程无法得到精确解;而CFD 就是通过采用各种计算方法得到这些偏微分方程的数值解,或称近似解。当然这些近似解应该满足一定的精度。目前,主要采用的CFD 方法是有限差分法和有限体积法。本讲主要介绍有限差分法,它也是下一讲中的有限体积法的基础[1]。 有限差分法求解流动控制方程的基本过程是:首先将求解区域划分为差分网格,用有限个网格点代替连续的求解域,将待求解的流动变量(如密度、速度等)存储在各网格点上,并将偏微分方程中的微分项用相应的差商代替,从而将偏微分方程转化为代数形式的差分方程,得到含有离散点上的有限个未知变量的差分方程组。求出该差分方程组的解,也就得到了网格点上流动变量的数值解。 2.1 差分和逼近误差 由于通常数字计算机只能执行算术运算和逻辑运算,因此就需要一种用算术运算来处理函数微分运算的数值方法。而有限差分法就是用离散网格点上的函数值来近似导数的一种方法。 设有x 的解析函数 )(xfy ,从微分学知道函数y 对x 的导数为 xxfxxfxydxdyxx)()(limlim00 (2-1) dy 、 dx 分别是函数及自变量的微分,dxdy /是函数对自变量的导数,又 称微商。相应地 ,上式中的x 、 y 分别称为自变量及函数的差分,xy /为函数对自变量的差商。在导数的定义 中x 是以 任 意 方式逼 近于零 的,因而x 是可 正 可 负 的。在差分方法中,x 总 是取 某 一小 的正 数。这样 一来,与 微分对应的差分可 以 有三 种形式: 向 前差分 )()(xfxxfy 向 后 差分 )()(xxfxfy 中心 差分 )21()21(xxfxxfy 上面 谈 的是一阶 导数,对应的称为一阶 差分。对一阶 差分再 作 一阶 差分,就得到二 阶 差分,记 为y2。以 前向 差分为例 ,有 应用计算流体力学讲稿 罗东明 2 )()(2)2()()()()2()()()()()(2xfxxfxxfxfxxfxxfxxfxfxxfxfxxfyy (2-2) 依次类推,任何阶差分都可以由低一阶再作一阶差分得到。 函数的差分与自变量的差分之比,即为函数对自变量的差商。如一阶向前差商为 xxfxxfxy)()( 一阶向后差商为 xxxfxfxy...