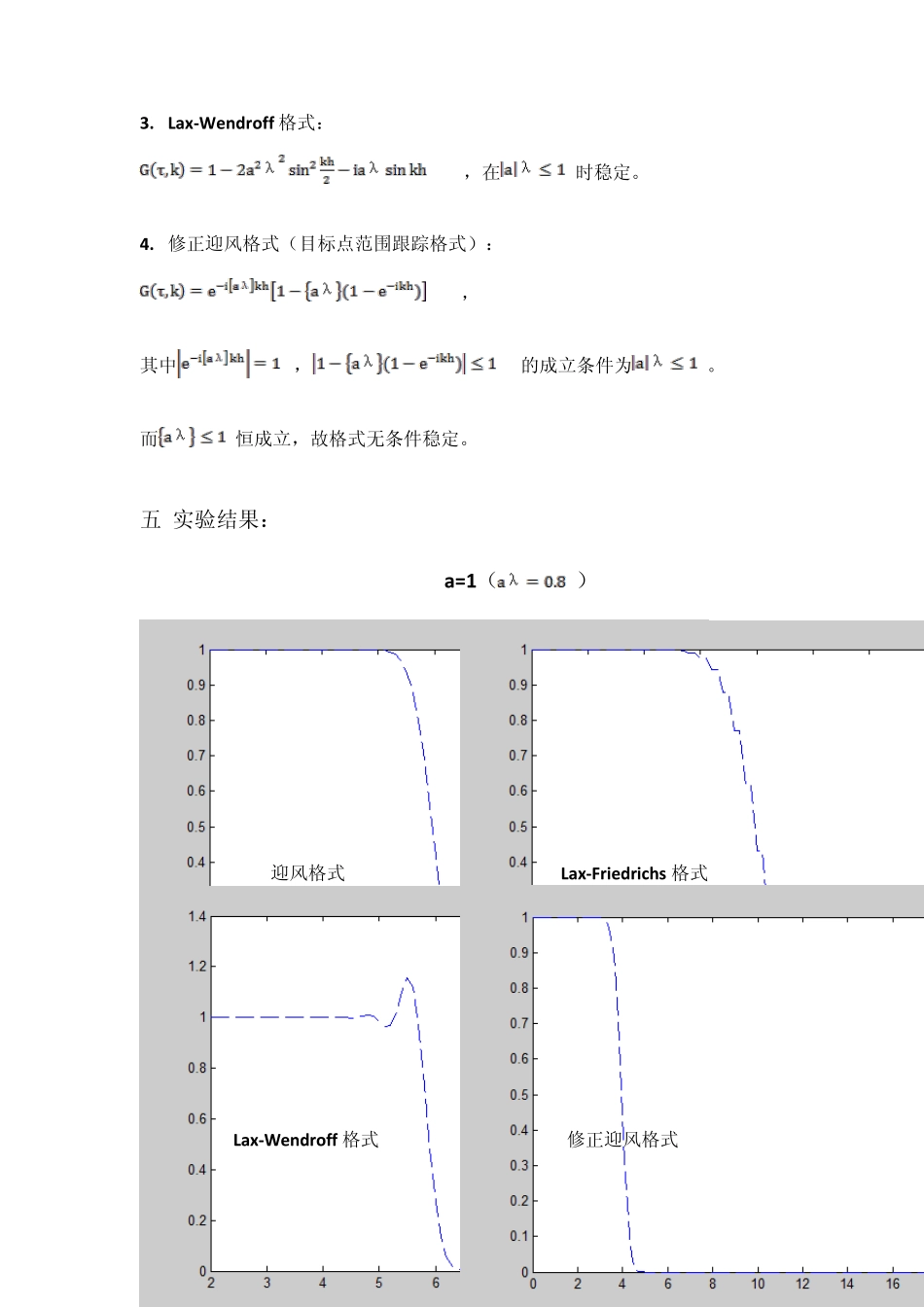
差分格式稳定性及数值效应比较实验 一 实验目的: 1.以一阶线性双曲线方程为例,使用Matlab 工具分析4 种差分格式的误差。 2.了解 4 种差分格式的稳定性。 二 实验问题: 对于一阶线性双曲型方程: 取 a=1,2,4, h=0.1, τ =0.08, 对不同的差分格式(迎风格式,Lax-Friedrichs 格式,Lax-Wendroff 格式,修正迎风格式)及不同的a 值进行迭代计算。通过将计算结果与精确解来进行比较,来讨论分析差分格式的稳定性。 三 实验原理: 1. 迎风格式: 这种格式的基本思想是简单的,就是在双曲型方程中关于空间偏导数用在特征线方向一侧的单边差商来代替,格式如下: 运算格式: 2. Lax-Friedrichs 格式: 运算格式: 3. Lax-Wendroff 格式: 这种格式构造是采用 Tay lor 级数展开和微分方程本身得到 运算格式: 4. 修正迎风格式(目标点范围跟踪格式): 其中是取整数部分,=。根据之后的理论分析可以得到这是一个无条件稳定结构。 四 四种格式理论分析: 通过求差分格式的增长因子 G(τ , k),来判定差分格式是否稳定。 1. 迎风格式: 记,则, 得, 即。 所以。 则在,满足 von Neumann 条件,格式稳定。 以下格式用相同方法求解稳定性条件。 2. Lax-Friedrichs 格式: ,在时稳定。 3. Lax-Wendroff 格式: ,在时稳定。 4. 修正迎风格式(目标点范围跟踪格式): , 其中,的成立条件为。 而恒成立,故格式无条件稳定。 五 实验结果: a=1() 迎风格式 Lax-Friedrichs 格式 Lax-Wendroff 格式 修正迎风格式 a=2( ) 迎风格式 Lax-Friedrichs 格式 Lax-Wendroff 格式 修正迎风格式 a=4( ) 迎风格式 Lax-Friedrichs 格式 Lax-Wendroff 格式 修正迎风格式 六 总结: 本次实验,通过4 种差分格式求解T=4 时的解并与解析解画图比较,可以看出: (1) a=1(aλ =0.8<1)时,迎风格式,Lax-Friedrichs 格式,修正迎风格式的计算结果与解析解近似情况较好,而Lax-Wendroff 格式则在间断点处出现了波前波,形成双波现象,这符合Lax-Wendroff 格式为二阶迭代格式的性质。 (2) a=2(aλ =1.6>1)时,迎风格式,Lax-Friedrichs 格式,Lax-Wendroff 格式都出现了比较强烈的震荡。这三种震荡中,Lax-Friedrichs 格式震荡较小,迎风格式与Lax-Wendroff 格式的震荡则较大。与之相对应的是修正迎风格式,保持着稳定的性质。 (3) a=4(aλ ...