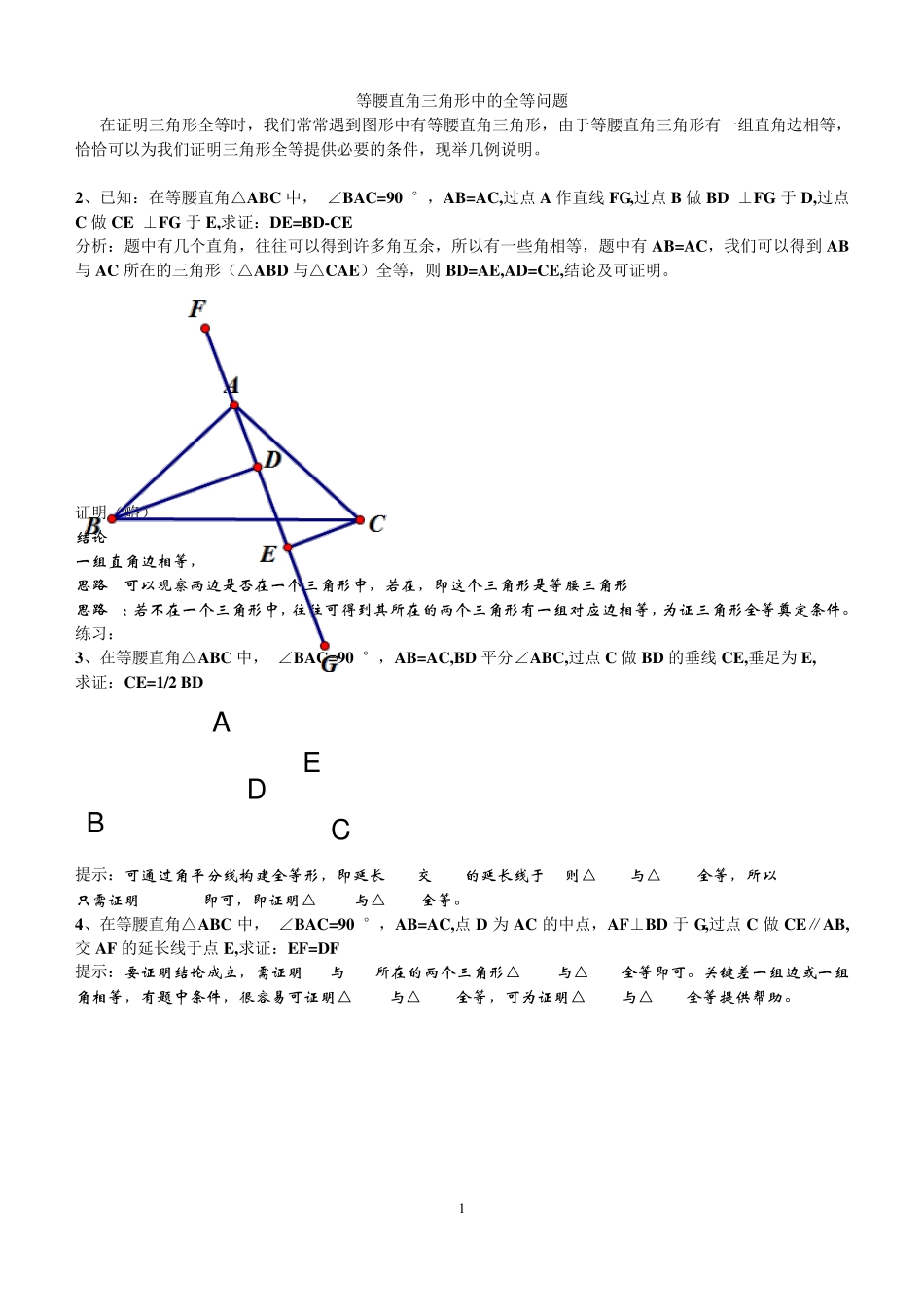
1 等腰直角三角形中的全等问题 在证明三角形全等时,我们常常遇到图形中有等腰直角三角形,由于等腰直角三角形有一组直角边相等,恰恰可以为我们证明三角形全等提供必要的条件,现举几例说明。 2、已知:在等腰直角△ABC 中, ∠BAC=90 °,AB=AC,过点 A 作直线 FG,过点 B 做 BD ⊥FG 于D,过点C 做 CE ⊥FG 于E,求证:DE=BD-CE 分析:题中有几个直角,往往可以得到许多角互余,所以有一些角相等,题中有AB=AC,我们可以得到AB与 AC 所在的三角形(△ABD 与△CAE)全等,则 BD=AE,AD=CE,结论及可证明。 证明(略) 结论: 一组直角边相等, 思路 1:可以观察两边是否在一个三角形中,若在,即这个三角形是等腰三角形 思路 2:若不在一个三角形中,往往可得到其所在的两个三角形有一组对应边相等,为证三角形全等奠定条件。 练习: 3、在等腰直角△ABC 中, ∠BAC=90 °,AB=AC,BD 平分∠ABC,过点 C 做 BD 的垂线 CE,垂足为E, 求证:CE=1/2 BD 提示:可通过角平分线构建全等形,即延长 CE交 BA的延长线于 F,则△BEF与△BEC全等,所以 CF=2CE,只需证明 CF=BD即可,即证明△ABD与△ACF全等。 4、在等腰直角△ABC 中, ∠BAC=90 °,AB=AC,点 D 为AC 的中点,AF⊥BD 于G,过点 C 做 CE∥AB,交 AF 的延长线于点 E,求证:EF=DF 提示:要证明结论成立,需证明 EF与 DF所在的两个三角形△CFD与△CFE全等即可。关键差一组边或一组角相等,有题中条件,很容易可证明△ABD与△CAE全等,可为证明△CFD与△CFE全等提供帮助。 C B A D E 2 5、如图,△ACD 和△AEB 都是等腰直角三角形,∠EAB=∠CAD=90°,求证: (1)EC=BD (2)EC⊥BD (3)BDECSEBCD 21四边形 (4)S△ADE=S△ABC 6、已知:在等腰直角△ABC 中, ∠BAC=90 °,AB=AC,E 为AC 上一点,CD⊥BE 于D,连接AD,若AD=2,CD=3,求BD 的长。 提示:由于等腰直角三角形的特征,把 CA绕点 A逆时针旋转 90°,即可与 BA重合,所以,可把 DA同样处理,使之旋转到点 E处,则△CAD与△BAE全等,即可得到结论。 在等腰直角△ABC中,∠ACB=90°,D是 AC中点,∠ADF=∠CDB,连接 CF交 BD于 E,求证:BD⊥CF. 7.(2011秋• 硚 口区期中)如图,在等腰直角△ABC中,∠ABC=90°,D为 AC的中点,过 D点作 DE⊥DF,交 AB于 E,交 BC于 F. 求证:(1)DE=DF (2) ∠DEF=45°. G B E C D A F A C ...