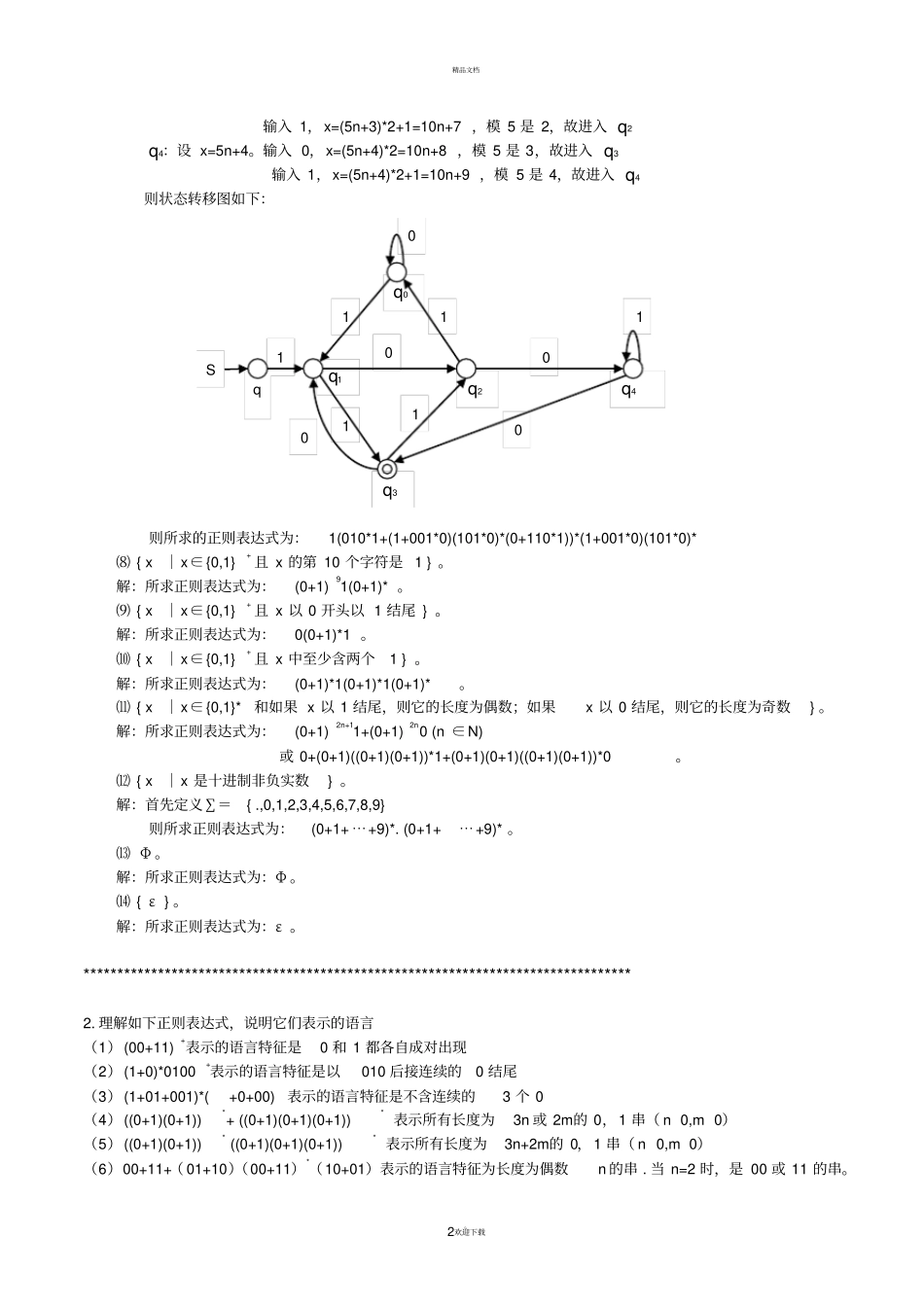
精品文档。1欢迎下载1. 写出表示下列语言的正则表达式。⑴ {0, 1}*。解:所求正则表达式为:(0+1)* 。⑵ {0, 1}+。解:所求正则表达式为:(0+1)+。⑶ { x│x∈ {0,1}+ 且 x 中不含形如00 的子串 } 。解:根据第三章构造的FA,可得所求正则表达式为:1*(01+)*(01+0+1)。⑷ { x│x∈ {0,1}*且 x 中不含形如00 的子串 } 。解:根据上题的结果,可得所求正则表达式为:ε+1*(01+)*(01+0+1)。⑸ { x│x∈ {0,1}+ 且 x 中含形如 10110 的子串 } 。解:所求正则表达式为:(0+1)*10110(0+1)*。⑹ { x│x∈ {0,1}+ 且 x 中不含形如10110 的子串 } 。解:根据第三章的习题,接受x 的 FA为:要求该 FA对应的正则表达式,分别以q0、 q1、 q2、q3、q4为终结状态考虑:q0为终态时的正则表达式:(0*(11*0(10)*(ε +111*11*0(10)*)0)*)* q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)* q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)* 将以上 5 个正则表达式用“+”号相连,就得到所要求的正则表达式。⑺ { x│x∈ {0,1}+ 且当把 x 看成二进制数时,x 模 5 与 3 同余和 x 为 0 时,│ x│=1 且 x≠0 时, x 的首字符为1} 。解:先画出状态转移图,设置5 个状态 q0、q1、q2、q3、q4,分别表示除5 的余数是 0、1、2、3、4 的情形。另外,设置一个开始状态q. 由于要求 x 模 5 和 3 同余,而 3 模 5 余 3, 故只有 q3 可以作为终态。由题设, x=0 时,│ x│=1,模 5 是 1,不符合条件,所以不必增加关于它的状态。下面对每一个状态考虑输入0 和 1 时的状态转移。q: 输入 1,模 5 是 1,进入 q1。q0: 设 x=5n。输入 0,x=5n*2=10n ,模 5 是 0,故进入 q0输入 1,x=5n*2+1=10n+1 ,模 5 是 1,故进入 q1q1:设 x=5n+1。输入 0,x=(5n+1)*2=10n+2 ,模 5 是 2,故进入 q2输入 1,x=(5n+1)*2+1=10n+3 ,模 5 是 3,故进入 q3q2:设 x=5n+2。输入 0,x=(5n+2)*2=10n+4 ,模 5 是 4,故进入 q4输入 1,x=(5n+2)*2+1=10n+5 ,模 5 是 0,故进入 q0q3:设 x=5n+3。输入 0,x=(5n+3)*2=10n+6 ,模 5 是 1,故进入 q1S 0 1 1 0...