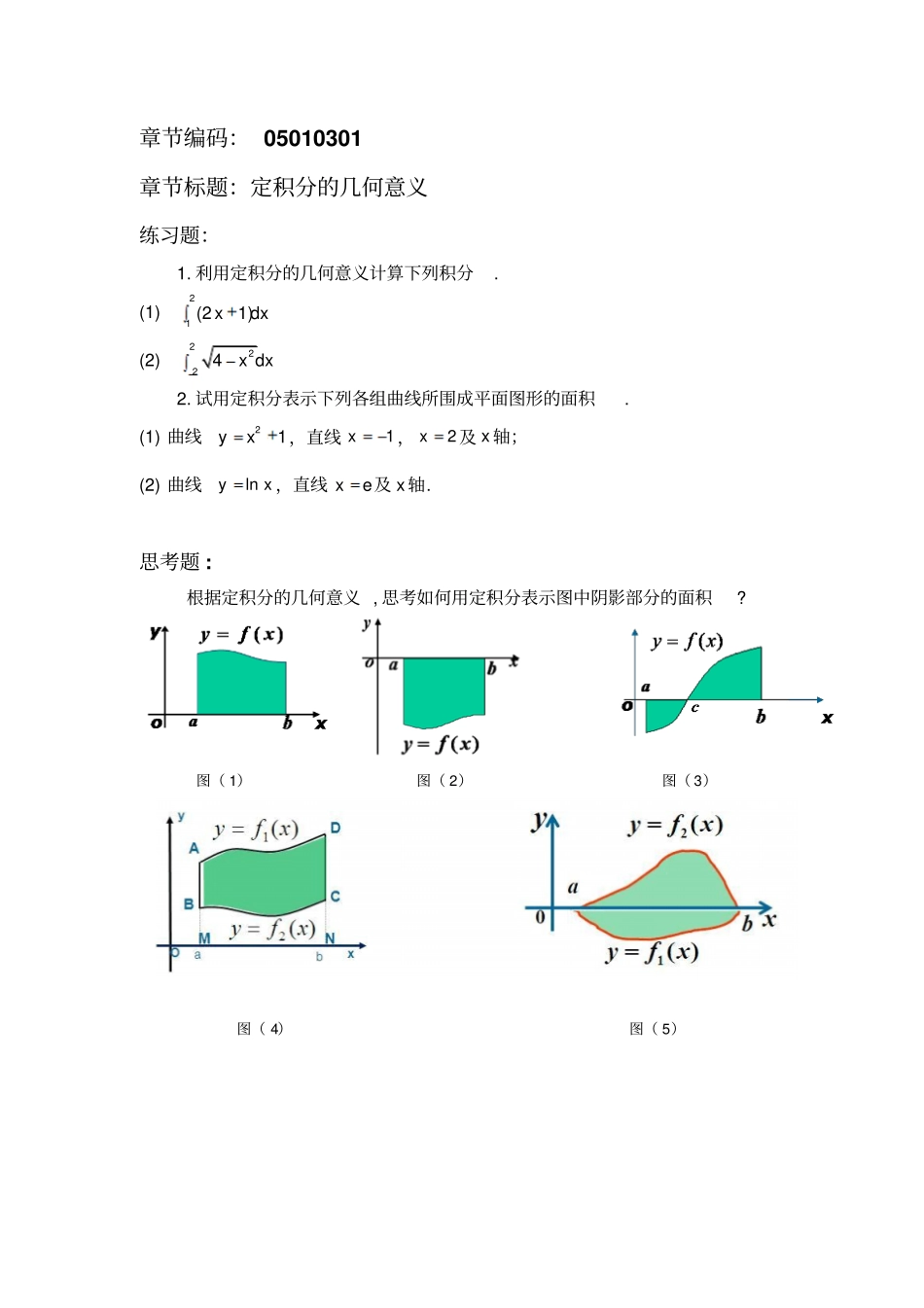
第五章微课配套练习题、思考题章节编码: 05010101章节标题:定积分问题举例思考题:定积分( ) dba f xx是表示由曲线( )fx ,,xa xb ,及 x 轴所围成的平面图形(此图形称为曲边梯形)的面积,对吗?章节编码: 05010201章节标题:定积分的定义练习题 : 1. 判断题(1)在定积分的定义中, 对积分区间 [ , ]a b 的分割,是指在区间 [ , ]a b 内插入1n个分点将区间 n 等分 . ()(2)若函数( )f x 在区间 [ , ]a b 上连续,则( )( )bbaaf x dxf t dx. ()(3)若函数( )f x 在区间 [0,1] 上可积,则1011( )lim()nnkkf x dxfn n . ()2. 填空题(1)设 S是由曲线2yx ,直线1,3,0xxy所围成的曲边梯形, 在区间 [1,3]内插入1n个分点将其 n 等分,则每个小区间的长度是 . (2)( )badf x dxdx . 思考题 : 利用定积分的定义来计算120 x dx的值 . 章节编码: 05010301章节标题:定积分的几何意义练习题:1. 利用定积分的几何意义计算下列积分. (1) 21 (21)xdx(2) 2224x dx2. 试用定积分表示下列各组曲线所围成平面图形的面积. (1) 曲线21yx,直线1x,2x及 x 轴;(2) 曲线lnyx ,直线 xe及 x 轴. 思考题 : 根据定积分的几何意义 , 思考如何用定积分表示图中阴影部分的面积? 图( 1)图( 2)图( 3)图( 4)图( 5)章节编码: 05010401 章节标题:定积分的线性性质练习题:1. 已知2( ),[( )]bbaaf x dxAf xdxB , 利用定积分的线性性质求下列式子的值. (1)[3( )4]baf xdx(2)24[( )1]bafxdx2. 计算10 (64)xdx思考题:已知函数( ),( )bbaaf x dxAg x dxB ,问下列解法对吗?1.( ) ( )( )( )bbbaaaf x g x dxf x dxg x dxAB2. 222( )[( )]bbaafx dxf x dxA章节编码: 05010402章节标题:定积分的区间可加性练习题:1. 已知21, 11( )2,12xxf xx, 求31( ).f x dx2. 计算30 1.x dx思考题 : 已知0322101 ,9,3x dxx dx求321.x dx章节编码: 05010403章节标题:定积分的不等式性质练习题:1. 不计算积分,比较下列各组积分值的大小. (1)22211xdxx dx与(2)2244sinxdxxdx与2. 估计定积分321 (3)xdx 的值 . 思考题:估计定积分220xxedx 的值 . 章节编码: 05010404章节标题:定积分的积分中值定理练习题:1. 计算函数( )f xx 在闭区间 [0, 2] 上的平均值 .2....