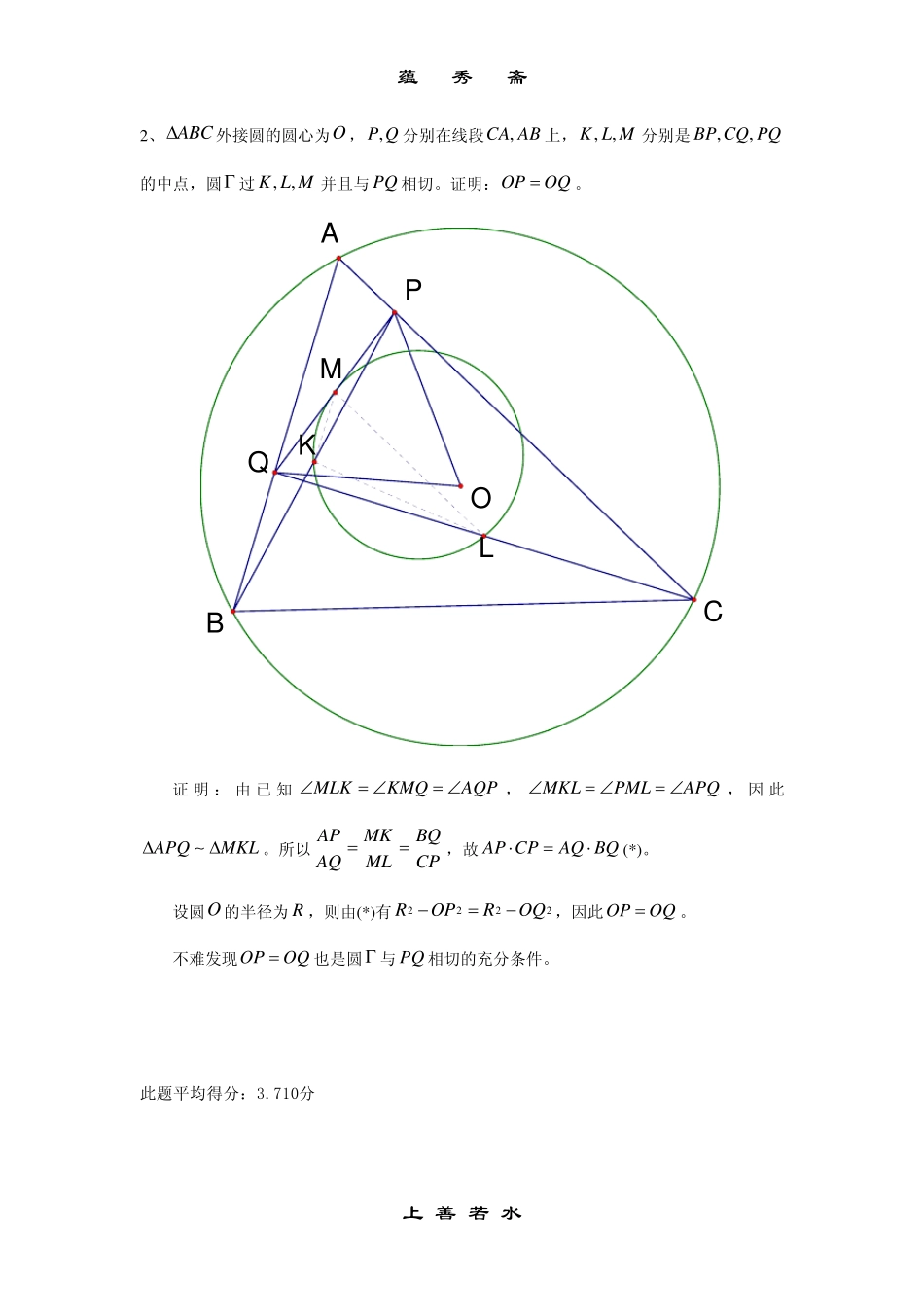
蕴 秀 斋 2009 年第50 届IMO解答 2 0 0 9 年7 月1 5 日 1 、是一个正整数,是n12,,...,(2 )ka aa k ≥{}1 ,2 ,...,n 中的不同整数,并且1(1iin a a+ − )−)对于所有都成立,证明:1 ,2 ,...,1ik=1(1ka a −不能被n 整除。 证明 1 :由于12(1n a a − ) ,令1( ,)n ap=,nqp=也是整数,则npq=,并且1p a ,21q a −。因此,由于2( ,)1q a=23(1npq a a)=−,故31q a −;同理可得41q a −,。。。,因此对于任意都有2i ≥1iq a − ,特别的有1kq a −,由于1p a ,故1 (1knpq a a)=−(*)。 若结论不成立,则1(1knpq a a=)−,与(*)相减可得1(kn aa−) ,矛盾。 综上所述,结论成立。 此题平均得分:4.804 分 上 善 若 水 蕴 秀 斋 2 、外接圆的圆心为O ,分别在线段上,ABC∆,P Q,CA AB, ,K L M 分别是,,BP CQ PQ的中点,圆过Γ, ,K L M 并且与相切。证明:OPPQOQ=。 KMLOBCAQP 证 明 : 由 已 知MLKKMQAQP∠= ∠= ∠,MKLPMLAPQ∠= ∠= ∠, 因 此APQMKL∆∆∼。所以 APMKBQAQMLCP==,故 AP CPAQ BQ⋅=⋅(*)。 设圆O 的半径为 R,则由(*)有2222ROPROQ−=−,因此OPOQ=。 不难发现OP也是圆Γ 与相切的充分条件。 OQ=PQ 此题平均得分:3.710分 上 善 若 水 蕴 秀 斋 3 、是 严 格 递 增 的 正 整 数 数 列 , 并 且 它 的 子 数 列和都是等差数列。证明:是一个等差数列。 123,,,...S SS123,,,...SSSSSS123111,,,.SSSSSS+++..123,,,...S SS问题等价于::fZZ+ →+ 是一个严格递增的函数。()( )nbff n=是一个等差数列,也是一个等差数列。证明:( ( ) 1ncff n=)+( )naf n=也是等差数列。 证 明 : 由 于是 一 个 严 格 递 增 的 整 值 函 数 , 所 以 对 于 任 意f,x y 均 有( )( )f xf yxy−≥−。 令{ } { },nnbc的公差分别为,则有,d e()()(1)( )(1)(dff nff nf nf n=+−≥+−) ,将可得( )nf n→()()( ) 1( )0nndff nff ncb≥+−=−>,因此对于任意都有 kZ +∈()()11110kkdcbcbk de++≥−=−+−> 故只能有,也即两个等差数列公差相等,故可设de=nncbg−=是一个为常数。 由于有界,故(1)( )0df nf n≥+−>(1)(f nf n)+−有最大最小值,设,M m 分别是的最大、最小值。则对任意(1)(f nf n+−),x y 都有( )( )m...