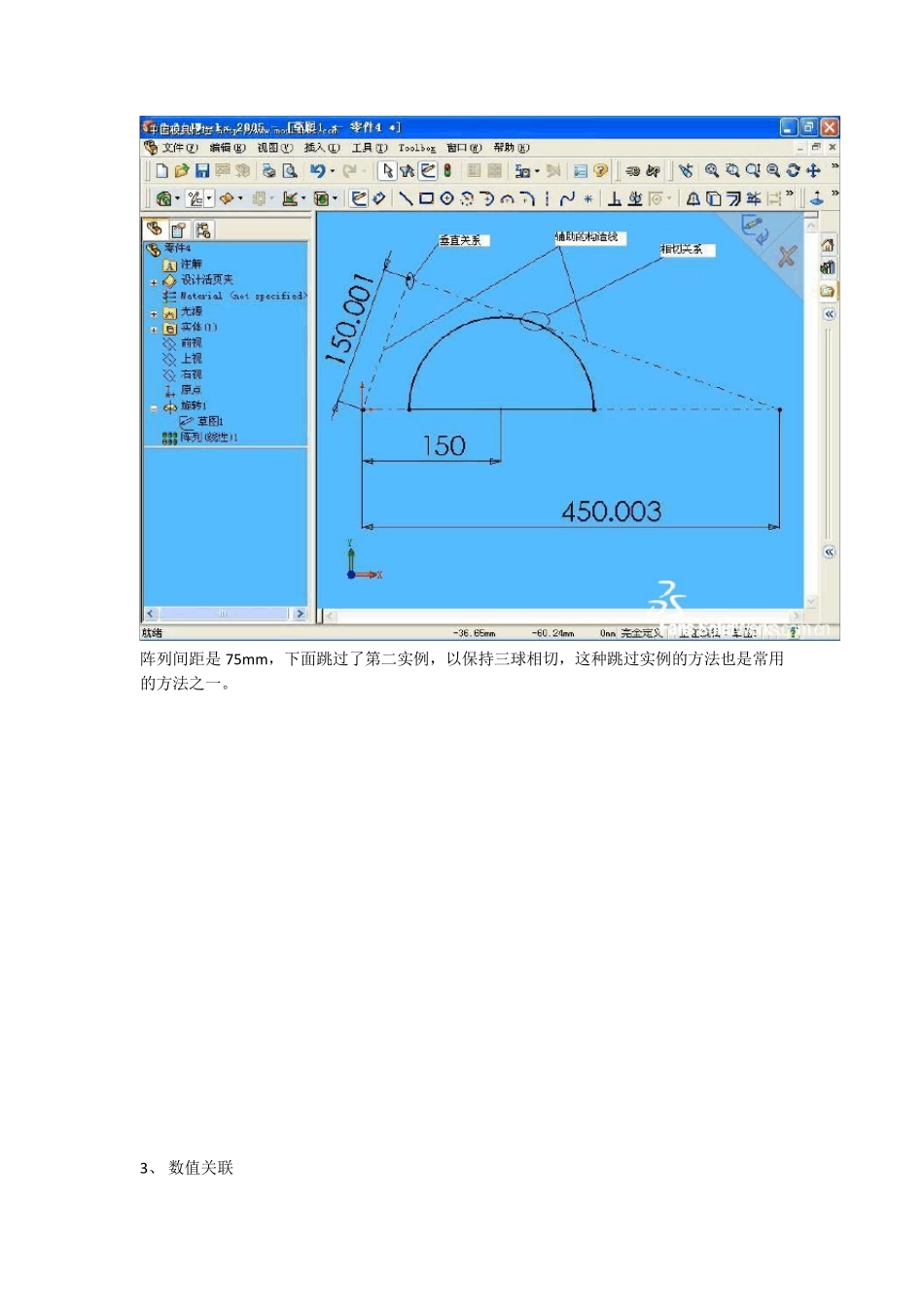
(本教程摘录自网上不老叔的精彩讲解) 随形阵列与一般阵列不同处是前者在阵列过程中其形状或位置会随着相关的特征、草图实体等而发生关联变化。使阵列千变万化,甚至于产生让人觉得不可思议的效果。 在驱动方式上,一般阵列有多种方式(习惯上多数用边线或基准轴驱动,并指定驱动方向),而随形阵列必需用尺寸驱动。如下图 阵列结果如下 复杂的随形阵列希望在尺寸驱动时,其它尺寸能同步作出变化,而且在SW 的阵列过程中方程式不起作用,这就需要用到一些窍门。下面列出一些常用的技术: 1、 使用辅助的构造线:草图上有些线条不是特征的实际轮廓线,但它能控制实际轮廓线的变化,一般用构造线画出。在复杂的随形阵列中由于要实现特殊的变化,就需要用更多的构造线。 2、 添加几何关系 下图中三个不等球相切。 草图中标出了辅助的构造线及几何关系,尺寸150.001 及 450.001 是考虑到让球的直半径增大 0.001mm是三个球能可靠相连。(如果分离将不能阵列特征) 阵列间距是75m m ,下面跳过了第二实例,以保持三球相切,这种跳过实例的方法也是常用的方法之一。 3、 数值关联 在随形阵列中,往往需要在驱动尺寸变化时,其它尺寸能关联变化。下图是一个薄壁圆锥筒上面有规则地嵌了许多小球,小球直径随着高度变化。 下图是在基准面上的一个草图,基准面时小球的所在平面,初始基准面距底面8.2m m ,按5.1m m 的间距向上阵列。关键是当基准面高度变化时保证小球中心在锥面上,并延着圆周方向旋转一定角度。 图中50、100、25 与锥筒的底半径、高、顶半径一致,中心距底面8.2m m 的尺寸与基准面高度对应,显然实线半圆的中心(即旋转后的小球中心)到原点中心的距离等于基准面高度的锥筒半径,这就保证了小球中心在锥筒壁上。尺寸8.2 左边的符号表明它是共享数据,在方程序下面说明名称为”1”的共享数值的初始值等于 8.2m m ,在此图中是一个线段和一个圆弧的长度,还有一个基准面高度未在此图中出现,由于共享数据的一致性,保证基准面高度不管如何变化,不会使小球离开筒壁。 图中的5 度线与半圆相切,使得小球的直径随着高度的增加而减少。 图中弧长 8.2m m 与基准面高度共享数据,使小球位置随着基准面高度的增加而顺时针转动,11.46m m 的半径决定了小球转动的快慢,半径越小,转动越快。 小球在圆周方向的阵列要在一个线性阵列中解决,那就不能用圆周阵列了,用线性阵列实现圆周阵列也是一种常用的手段...