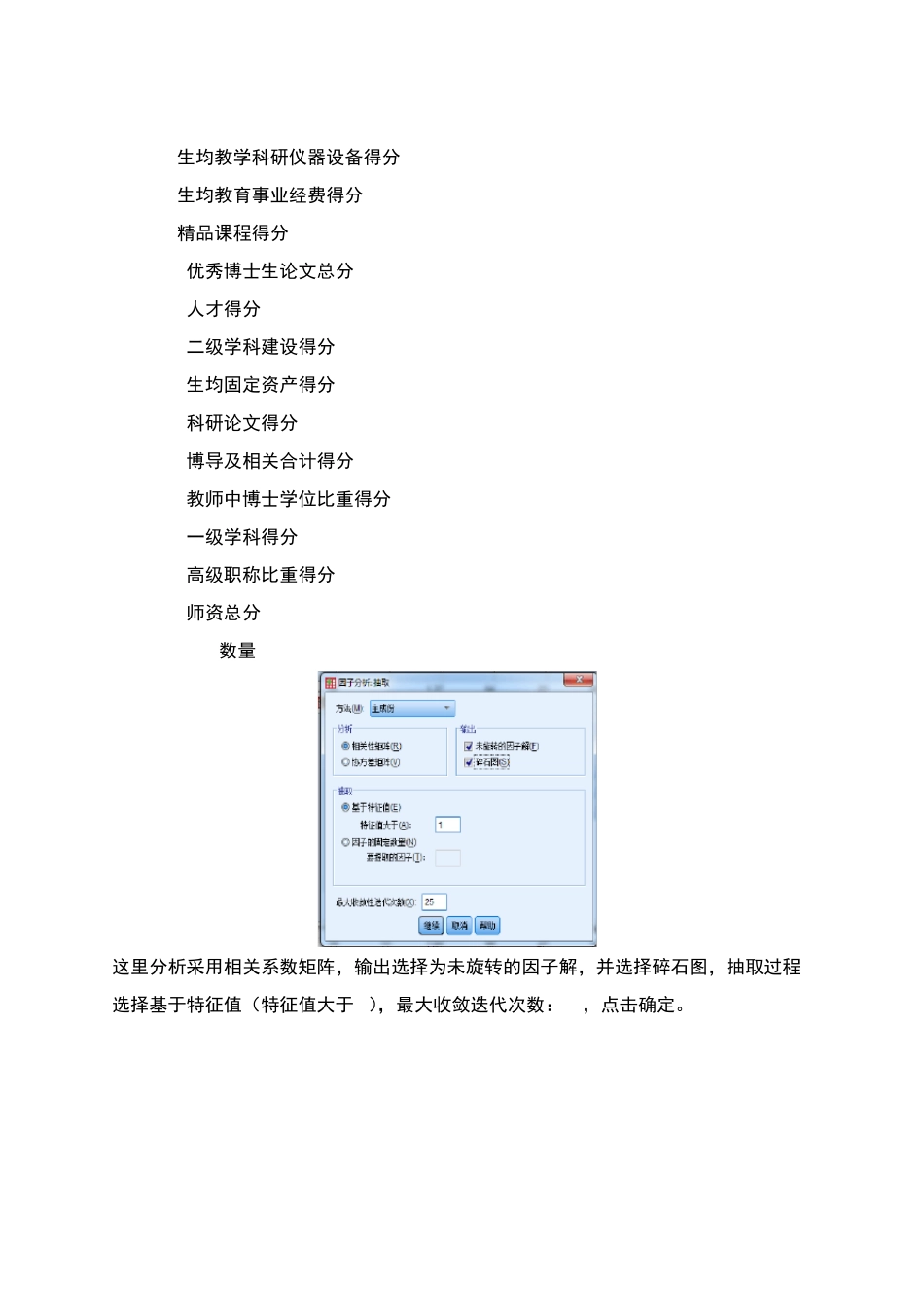
实用标准文档 文案大全 实验目的:原始数据中每一所高校具有20个相关性很高的变量,利用主成分分析法用较少的变量去解释原来资料中的大部分变异,将手中的众多变量转化成彼此相互独立或不相关的个数较少的变量,即所谓主成分,并用以解释资料的综合性指标,其实质的目的是降维 原始数据截屏: 操作方法: 1. 描述性统计 SPSS在调用因子分析过程进行分析时,SPSS会自动对原始数据进行标准化处理,所以在得到计算结果后指的变量都是指经过标准化处理后的变量,但SPSS不会直接给出标准化后的数据,然后后期的计算需得到标准化数据,则需调用“描述”过程进行计算,为了看到标准化数据,所以采用描述性统计下的描述操作获得标准化后的变量数据 标准化数据: 因子分析操作过程: 选取变量: X1:科研经费得分 X2:国家人文社科重点研究基地得分 X3:院士总数得分 X4:生均图书得分 X5:研究中心数得分 X6:国家重点实验室得分 X7:生均教学科研仪器设备得分 X8:生均教育事业经费得分 X9:精品课程得分 X10:优秀博士生论文总分 X11:人才得分 X12:二级学科建设得分 X13:生均固定资产得分 X14:科研论文得分 X15:博导及相关合计得分 X16:教师中博士学位比重得分 X17:一级学科得分 X18:高级职称比重得分 X19:师资总分 X20:SCI数量 这里分析采用相关系数矩阵,输出选择为未旋转的因子解,并选择碎石图,抽取过程选择基于特征值(特征值大于1),最大收敛迭代次数:25,点击确定。 原数据中有较多的缺失值,选择按列表排除个案,点击继续。 分析结果: KMO越接近 1,说明变量之间的相关性越强,原有变量适合做因子分析;Bartlett的球度检验值越小于显著性水平 0.05,越说明变量间存在相关关系。 本数据中KMO值为 0.736,sig.值为 0,符合因子分析条件,可进行因子分析,并进一步进行主成分分析 累计贡献率79.119%<80%,由反映象相关矩阵中我们可以看出(如下图所示) 反映象相关矩阵中对角线上的数值应>0.5,根据次标准,数据显示生均图书得分变量不适合做因子分析,所以删去,重新做因子分析。 去除生均图书得分变量之后的因子分析结果: 累计百分比为81.466%>80%,且特征值均大于1 结论: 初始特征根:λ1=6.901,,λ2=4.846,λ3=3.732 主成分贡献率:r1=36.32%,r2=25.506%,r3=19.640% 碎石图 旋转之后的主成分载荷矩阵,可以看出:SCI数量,国家重点实验室得分,研究中心数得分,研究中心数得分,科研经费得分,二...