二项式系数的性质VIP免费

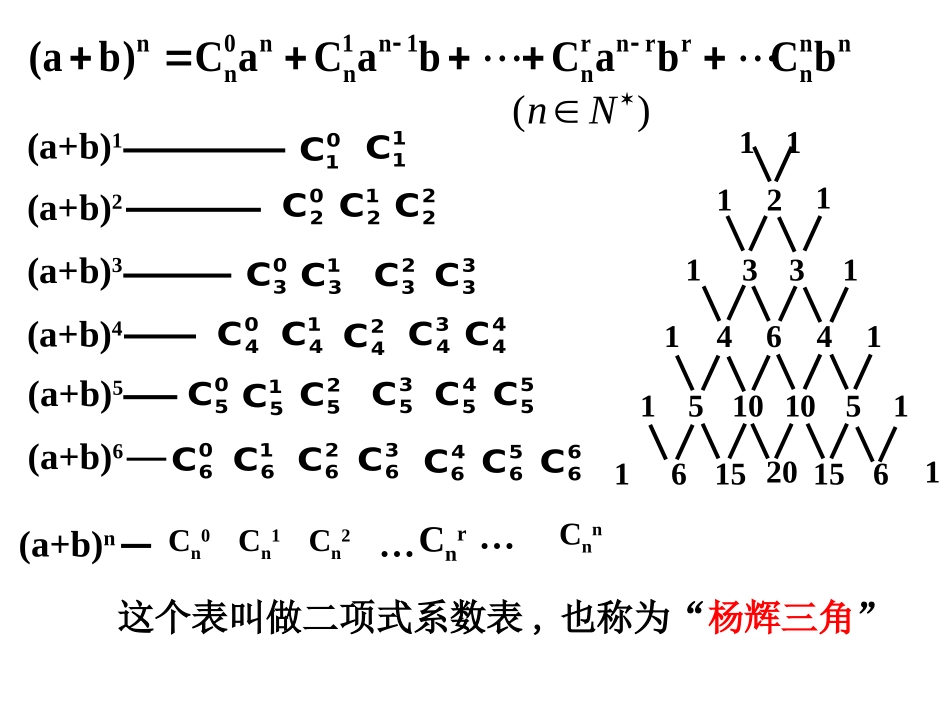
二项式定理----二项式系数的性质1615201561(a+b)1(a+b)3(a+b)4(a+b)5(a+b)201C11C02C12C22C03C13C23C33C05C15C25C35C45C55C(a+b)61112113311464115101051(a+b)n04C14C24C34C44CCn0Cn1Cn2CnrCnn……这个表叫做二项式系数表,也称为“杨辉三角”nnnrrnrn1n1nn0nnbCbaCbaCaC)ba()(Nn06C16C26C36C46C56C66C早在我国南宋数学家杨辉1261年所著的《详解九章算法》二项式系数表.在书中说明了表里“一”以外的每一个数都等于它肩上两个数的和；指出这个方法出于《释锁》算书，且我国北宋数学家贾宪（约公元11世纪）已经用过它.这表明我国发现这个表不晚于11世纪；在欧洲，这个表被认为是法国数学家帕斯卡（1623-1662）首先发现的，他们把这个表叫做帕斯卡三角.这就是说，杨辉三角的发现要比欧洲早五百年左右.《九章算术》杨辉《详解九章算法》中记载的表本积平方立方三乘四乘五乘商实二项式系数的函数观点：展开式的二项式系数依次是：nnnnnC,,C,C,C210从函数角度看，可看成是以r为自变量的函数：rnC当n=6时，其图象是7个孤立点！定义域是{0,1,2,…,n}rnCrf)(讲授新课：二项式系数的性质1：对称性与首末两端“等距离”的两个二项式系数相等．（正数第K项与倒数第K项)这一性质可直接由公式得到．mnnmnCC图象的对称轴：2nr一般地，展开式的二项式系数有如下性质：nba)(nnnnCCC,,10（2）mnmnmnCCC1116152015611112113311464115101051递推性：除1以外的每个数都等于它肩上两个数的和.2.若（a+b）n的展开式中，第三项的二项式系数与第五项的二项式系数相等，则n=_____.课堂练习1：课堂练习1：1.在(a＋b)n展开式中，与第k项二项式系数相等是第几项？61(1)(2)(1)1CC(1)!kknnnnnnknkkkk由于所以相对于的增减情况由决定．knC1Cknkkn1二项式系数的性质2：增减性与最大值11012222110122212CCC112)22C