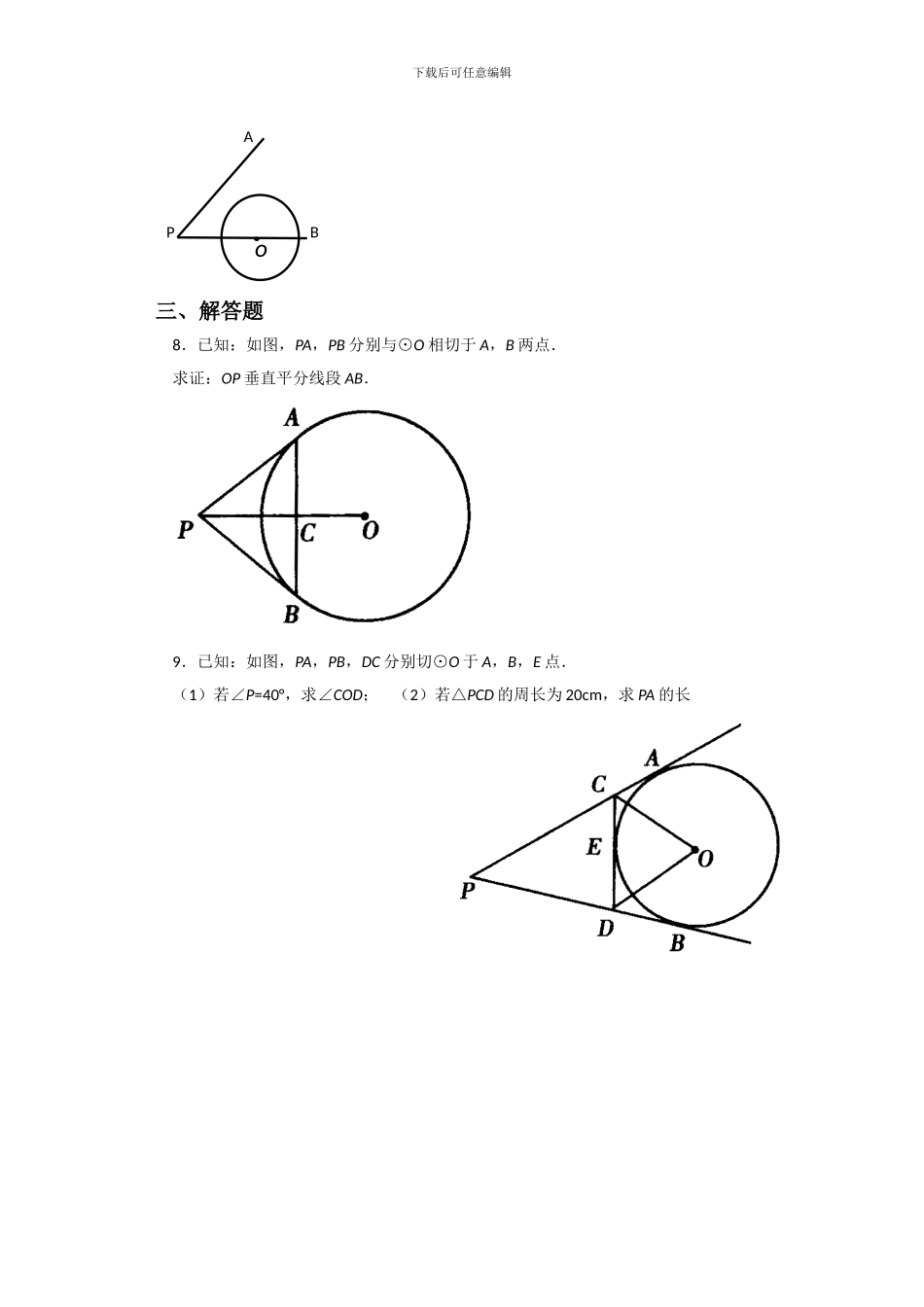
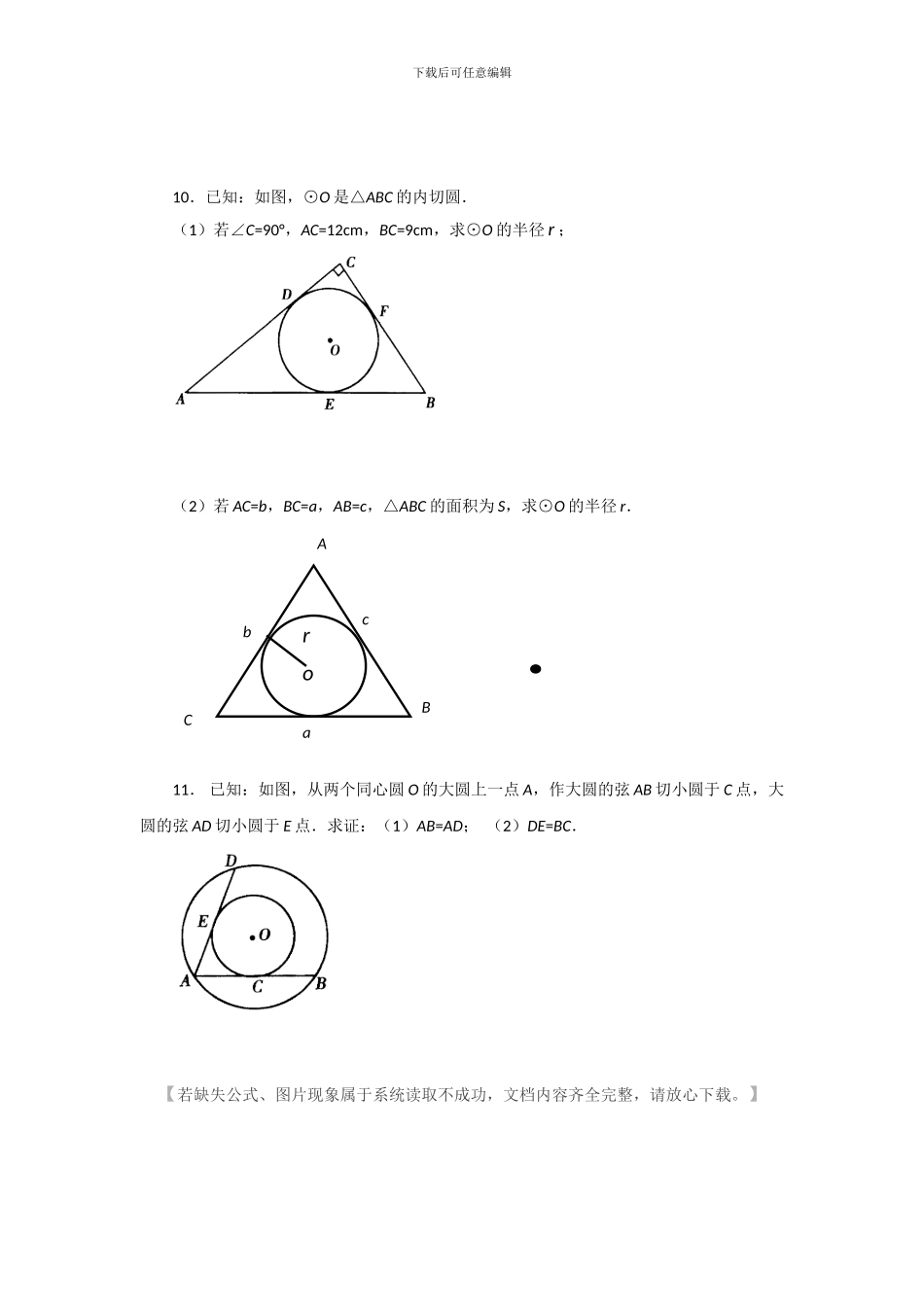
下载后可任意编辑《切线长定理》习题一、选择题1.⊙O 是△ABC 的内切圆,∠ACB=90°,∠BOC=105°,BC=20cm,则 AC=( )A.20cm B.20 C.40cm D.15cm2.已知:如图,AB、AC 分别切⊙O 于 B、C,D 是⊙O 上一点,∠D=40°,则∠ACB 的度数等于( ) A.40° B120° C. 100° D. 80°3.如图 1,PA、PB 分别切圆 O 于 A、B 两点,C 为劣弧 AB 上一点,∠APB=30°,则∠ACB=( ). A.60° B.75° C.105° D.120° (1) (2) (3) 二、填空题4.如图 2,PA、PB 分别切圆 O 于 A、B,并与圆 O 的切线,分别相交于 C、D,已知PA=7cm,则△PCD 的周长等于_________.5.如图 3,圆 O 内切 Rt△ABC,切点分别是 D、E、F,则四边形 OECF 是_______.6.如图 3,圆 O 内切 Rt△ABC,切点分别是 D、E、F,若⊙o 的半径 OF=2,AB=10,则△ABC 的面积是 7.如图, ∠APB=75°,OP=4cm,⊙o 的半径为 2cm,射线 PA 绕点 P 作顺时针旋转,当旋转 度时,PA 与相切.下载后可任意编辑三、解答题8.已知:如图,PA,PB 分别与⊙O 相切于 A,B 两点.求证:OP 垂直平分线段 AB.9.已知:如图,PA,PB,DC 分别切⊙O 于 A,B,E 点.(1)若∠P=40°,求∠COD; (2)若△PCD 的周长为 20cm,求 PA 的长PABo下载后可任意编辑10.已知:如图,⊙O 是△ABC 的内切圆.(1)若∠C=90°,AC=12cm,BC=9cm,求⊙O 的半径 r ; (2)若 AC=b,BC=a,AB=c,△ABC 的面积为 S,求⊙O 的半径 r.11. 已知:如图,从两个同心圆 O 的大圆上一点 A,作大圆的弦 AB 切小圆于 C 点,大圆的弦 AD 切小圆于 E 点.求证:(1)AB=AD; (2)DE=BC.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。】 ABCabcro下载后可任意编辑《切线长定理》分层练习◆ 基础题1.如图,PA、PB 切⊙O 于点 A、B,PA=10,CD 切⊙O 于点 E,交 PA、PB 于 C、D两点,则△PCD 的周长是( )A.10 B.18 C.20 D.222.如图,PA,PB 分别是⊙O 的切线,A,B 分别为切点,点 E 是⊙O 上一点,且∠AEB=60°,则∠P 为( )A.120° B.60° C.30° D.45°3.已知 P 为⊙O 外一点,PA,PB 为⊙O 的切线,A、B 为切点,∠P=70°,C 为⊙O上一个动点,且不与 A、B 重合,则∠BCA=( )A.35°C、145° B.110...