二次根式习题及答案VIP免费

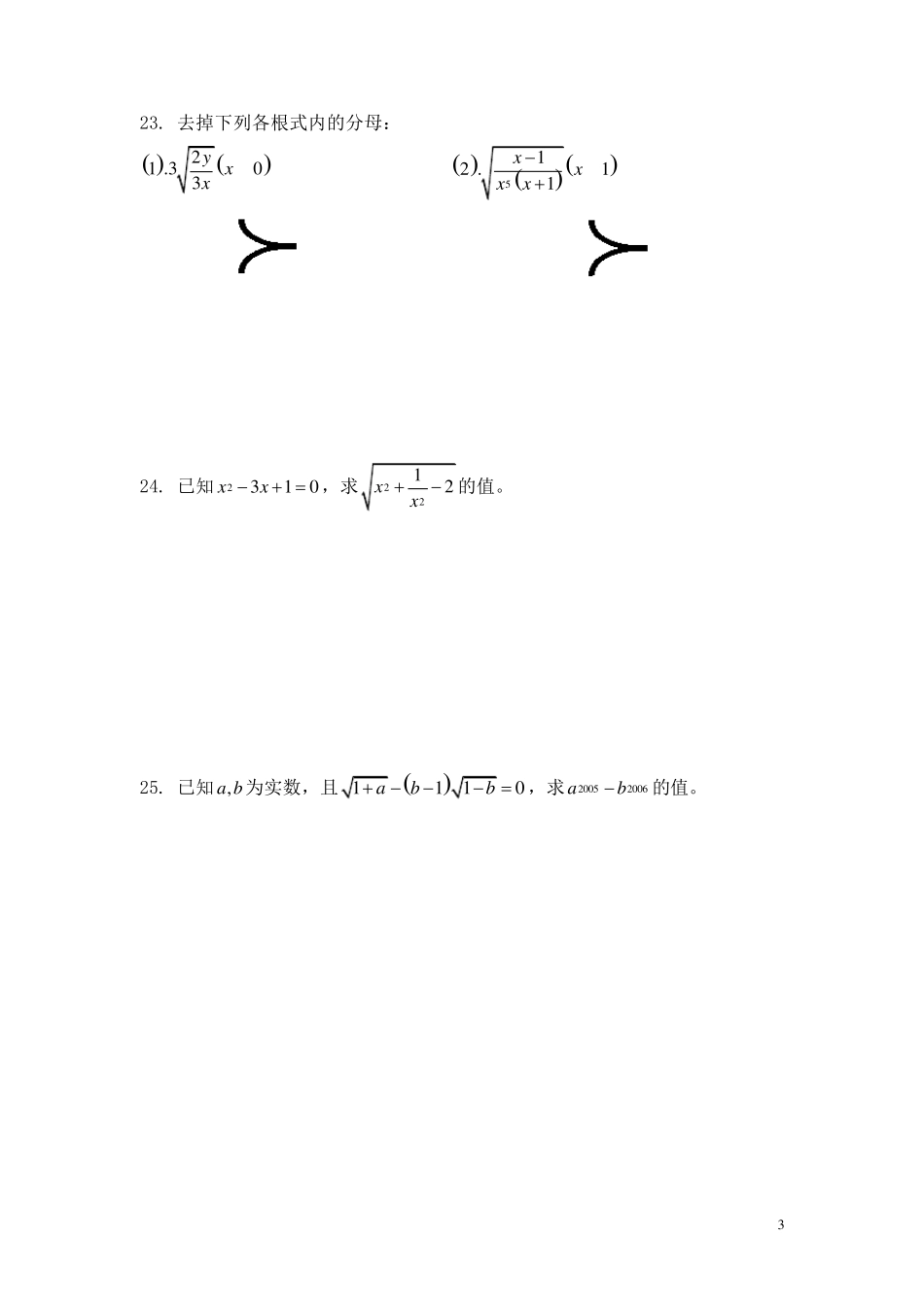
1 二次根式精选习题 21.1 二次根式： 1. 使式子4x有意义的条件是 。 2. 当 _ _ _ _ _ _ _ _ _ _ 时，212xx有意义。 3. 若11mm 有意义，则m 的取值范围是 。 4. 当_ _ _ _ _ _ _ _ _ _x时， 21x是二次根式。 5. 在实数范围内分解因式：429_ _ _ _ _ _ _ _ _ _ ,222_ _ _ _ _ _ _ _ _ _xxx。 6. 若242xx，则 x的取值范围是 。 7. 已知 222xx，则 x的取值范围是 。 8. 化简：2211xxx的结果是 。 9. 当15x时， 215_ _ _ _ _ _ _ _ _ _ _ _ _xx。 10. 把1aa的根号外的因式移到根号内等于 。 11. 使等式1111xxxx 成立的条件是 。 12. 若1ab 与24ab互为相反数，则2 0 0 5_ _ _ _ _ _ _ _ _ _ _ _ _ab。 13. 在式子230 ,2 ,12 ,20 , 3 ,1 ,2x xyyx xxx y 中，二次根式有（ ） A. 2 个 B. 3 个 C. 4 个 D. 5 个 14. 下列各式一定是二次根式的是（ ） A. 7 B. 3 2 m C. 21a  D. ab 15. 若 23a，则 2223aa等于（ ） A. 52 a B. 12 a C. 25a  D. 21a  16. 若424Aa，则A （ ） A. 24a  B. 22a  C. 222a  D. 224a  2 17. 若1a  ，则31a化简后为（ ） A. 11aa B. 11aa C. 11aa D. 11aa 18. 能使等式22xxxx成立的x 的取值范围是（ ） A. 2x  B. 0x  C. 2x D. 2x  19. 计算：222112aa的值是（ ） A. 0 B. 42a  C. 24 a D. 24 a或42a  20. 下面的推导中开始出错的步骤是（ ）     2223231 2123231 2223233224   A.  1 B.  2 C.  3 D.  4 21. 若2440xyyy，求xy的值。 22. 当 a 取什么值时，代数式211a   取值最小，并求出这个最小值。 3 23. 去掉下列各根式内的分母：  21 .303y xx  512 .11xxxx 24. 已知2310xx ，求2212xx的值。 25. 已知,a b为实数，且1110abb...