二阶电路响应实验报告VIP免费

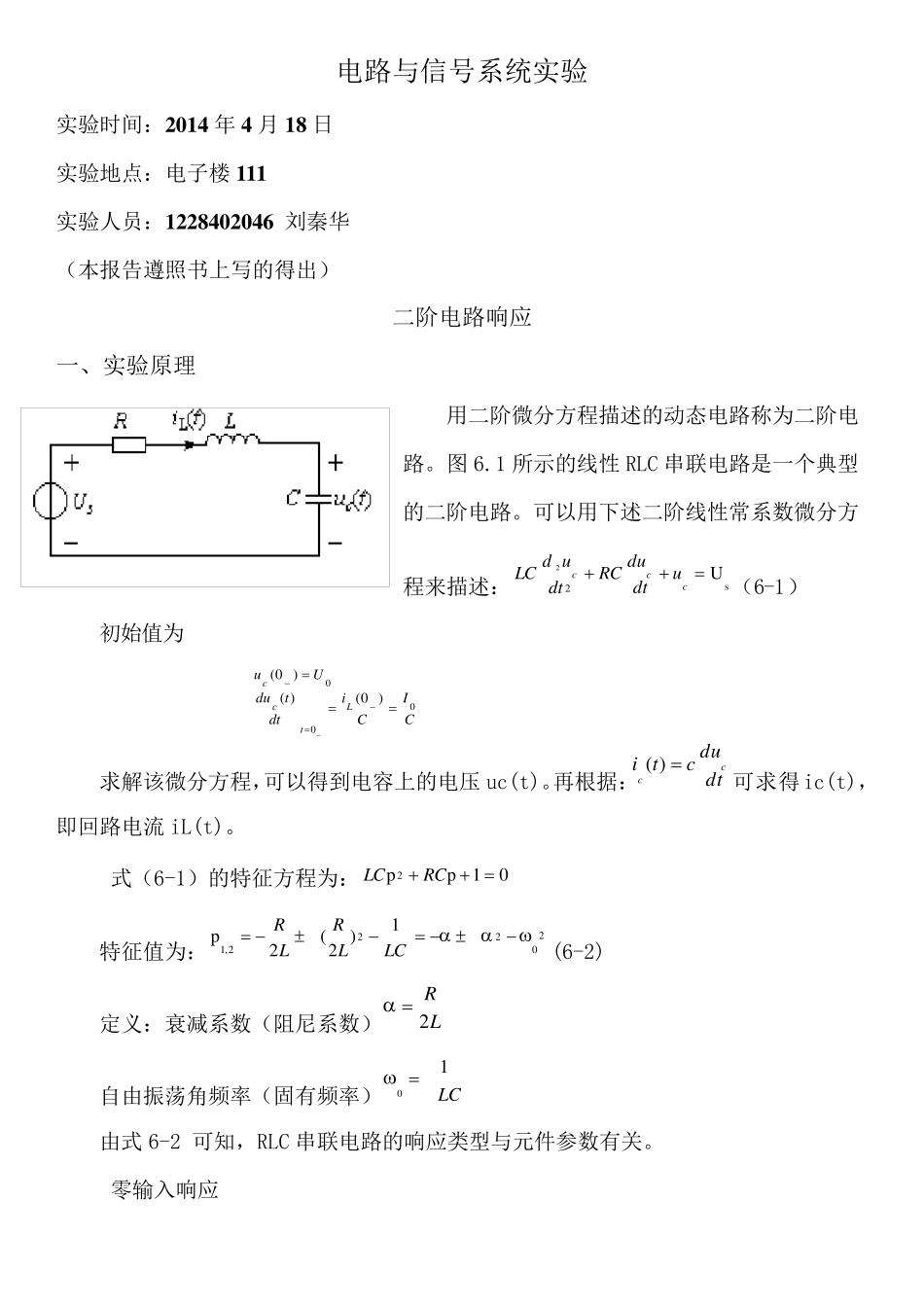
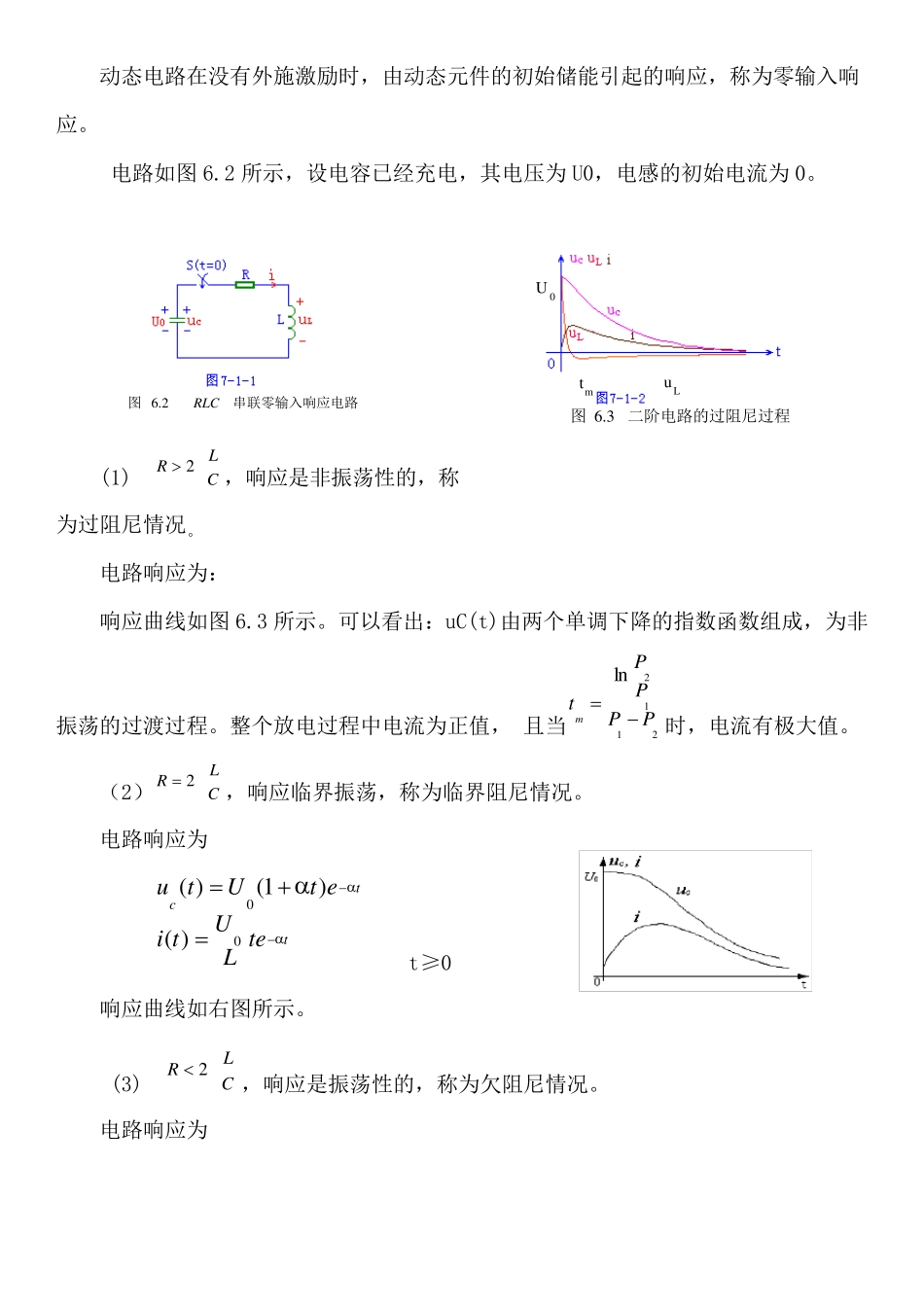
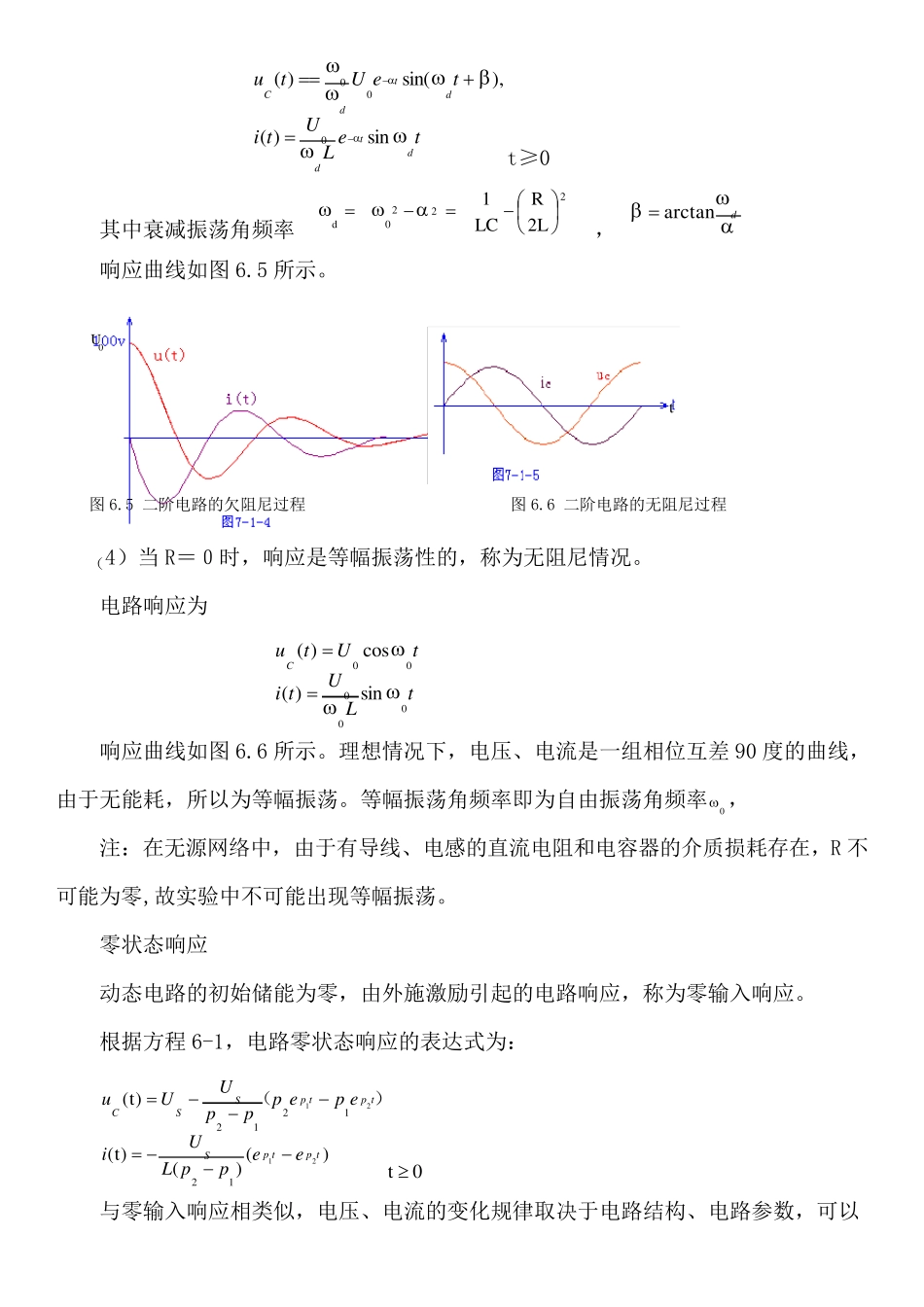
电路与信号系统实验 实验时间：2 0 1 4 年4 月1 8 日 实验地点：电子楼1 1 1 实验人员：1 2 2 8 4 0 2 0 4 6 刘秦华 （本报告遵照书上写的得出） 二阶电路响应 一、实验原理 用二阶微分方程描述的动态电路称为二阶电路。图 6.1 所示的线性 RLC 串联电路是一个典型的二阶电路。可以用下述二阶线性常系数微分方程来描述：s2U2cccudtduRCdtudLC（6-1） 初始值为 CICidttduUuLtcc000)0()()0( 求解该微分方程，可以得到电容上的电压 uc(t)。再根据：dtducticc)(可求得ic(t)，即回路电流 iL(t)。 式（6-1）的特征方程为：01pp 2 RCLC 特征值为：20222,11)2(2pLCLRLR(6-2) 定义：衰减系数（阻尼系数）LR2 自由振荡角频率（固有频率）LC10  由式 6-2 可知，RLC 串联电路的响应类型与元件参数有关。 零输入响应 动态电路在没有外施激励时，由动态元件的初始储能引起的响应，称为零输入响应。 电路如图6.2 所示，设电容已经充电，其电压为U0，电感的初始电流为0。 (1) CLR2，响应是非振荡性的，称为过阻尼情况。 电路响应为： 响应曲线如图6.3 所示。可以看出：uC(t)由两个单调下降的指数函数组成，为非振荡的过渡过程。整个放电过程中电流为正值， 且当2112lnPPPPtm时，电流有极大值。 （2）CLR2，响应临界振荡，称为临界阻尼情况。 电路响应为 ttcteLUtietUtu00)()1()( t≥0 响应曲线如右图所示。 (3) CLR2，响应是振荡性的，称为欠阻尼情况。 电路响应为 图6.2 RLC串联零输入响应电路 图6.3 二阶电路的过阻尼过程 u L tm U 0 teLUtiteUtudtddtdCsin)(),sin()(000t≥0 其中衰减振荡角频率 2220d2LRLC1 ， darctan 响应曲线如图 6.5 所示。 U0 t 图 6.5 二阶电路的欠阻尼过程 图 6.6 二阶电路的无阻尼过程 （4）当 R＝０时，响应是等幅振荡性的，称为无阻尼情况。 电路响应为 tLUtitUtuC00000sin)(cos)( 响应曲线如图 6.6 所示。理想情况下，电压、电流是一组相位互差 90 度的曲线，由于无能耗，所以为等幅振荡。等幅振荡角频率即为自由振荡角频率0 ， 注：在无源网络中，由于有导线、电感的直流电阻和电容器的介质损耗存在，R 不可能为零,故实验中不可能出现等幅振荡。 零状态...