二阶电路的动态响应实验报告2VIP免费

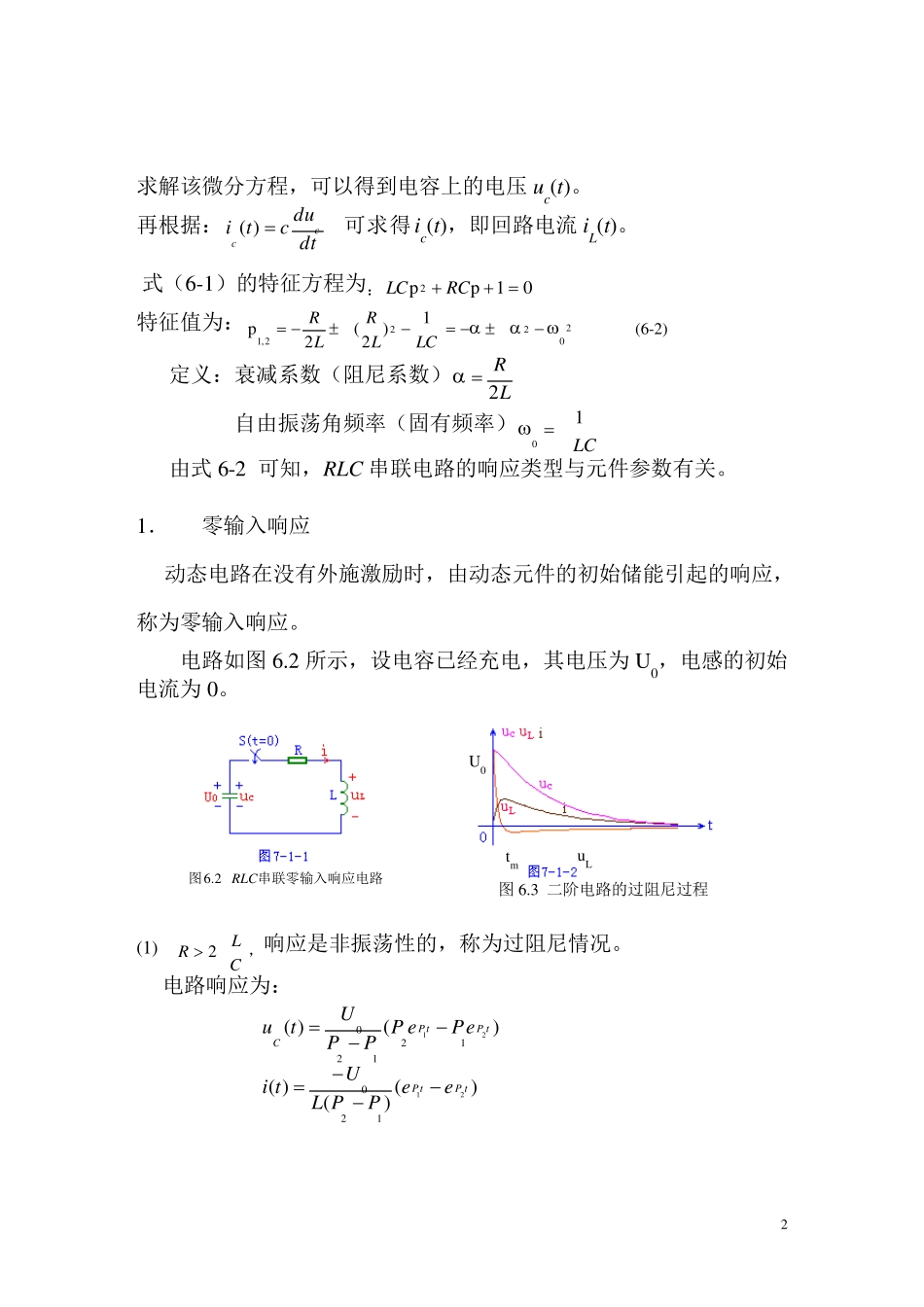
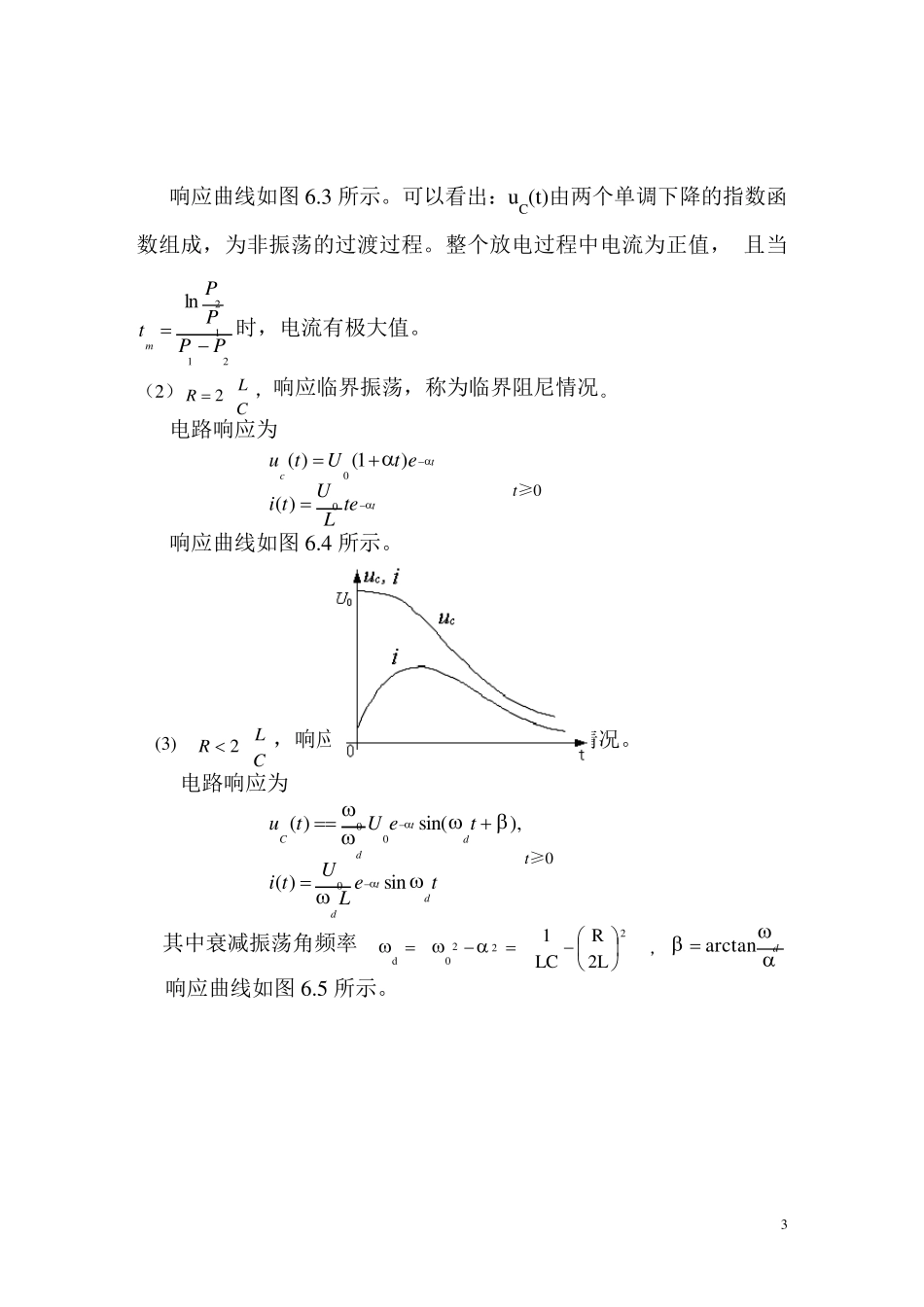
1 二阶电路的动态响应 一、实验目的： 1、学习用实验的方法来研究二阶动态电路的响应。 2、研究电路元件参数对二阶电路动态响应的影响。 3、研究欠阻尼时，元件参数对α 和固有频率的影响。 4、研究 RLC串联电路所对应的二阶微分方程的解与元件参数的关系。 二、实验仪器 数字万用表、模拟电路实验箱（AEDK-AEC）、示波器 DS1052E、信号发生器 EE1641D、导线、电阻、电位器、电感、电容、面包板等。 三、实验概述 1、实验原理 图 6.1 RLC 串联二阶电路 用二阶微分方程描述的动态电路称为二阶电路。图 6.1 所示的线性RLC 串联电路是一个典型的二阶电路。可以用下述二阶线性常系数微分方程来描述： s2U2cccudtduRCdtudLC （6-1） 初始值为 CICidttduUuLtcc000)0()()0( 2 求解该微分方程，可以得到电容上的电压u c(t)。 再根据：dtducticc)( 可求得ic(t)，即回路电流 iL(t)。 式（6-1）的特征方程为：01pp 2 RCLC 特征值为：20222,11)2(2pLCLRLR (6-2) 定义：衰减系数（阻尼系数）LR2 自由振荡角频率（固有频率）LC10  由式 6-2 可知，RLC 串联电路的响应类型与元件参数有关。 1． 零输入响应 动态电路在没有外施激励时，由动态元件的初始储能引起的响应，称为零输入响应。 电路如图 6.2 所示，设电容已经充电，其电压为 U0，电感的初始电流为 0。 (1) CLR2，响应是非振荡性的，称为过阻尼情况。 电路响应为： )()()()()(212112012120tPtPtPtPCeePPLUtiePePPPUtu 图6.2 RLC串联零输入响应电路 图 6.3 二阶电路的过阻尼过程 u L tm U0 3 响应曲线如图6.3 所示。可以看出：u C(t)由两个单调下降的指数函数组成，为非振荡的过渡过程。整个放电过程中电流为正值， 且当2112lnPPPPtm时，电流有极大值。 （2）CLR2，响应临界振荡，称为临界阻尼情况。 电路响应为 ttcteLUtietUtu00)()1()( t≥0 响应曲线如图6.4 所示。 图6.4 二阶电路的临界阻尼过程 (3) CLR2，响应是振荡性的，称为欠阻尼情况。 电路响应为 teLUtiteUtudtddtdCsin)(),sin()(000t≥0 其中衰减振荡角频率 2220d2LRLC1 ， darctan 响应曲线如图6.5 所示。 4 U0 t 图6.5 二阶电路的欠阻尼过程 图6.6 二阶电路的无阻尼过...