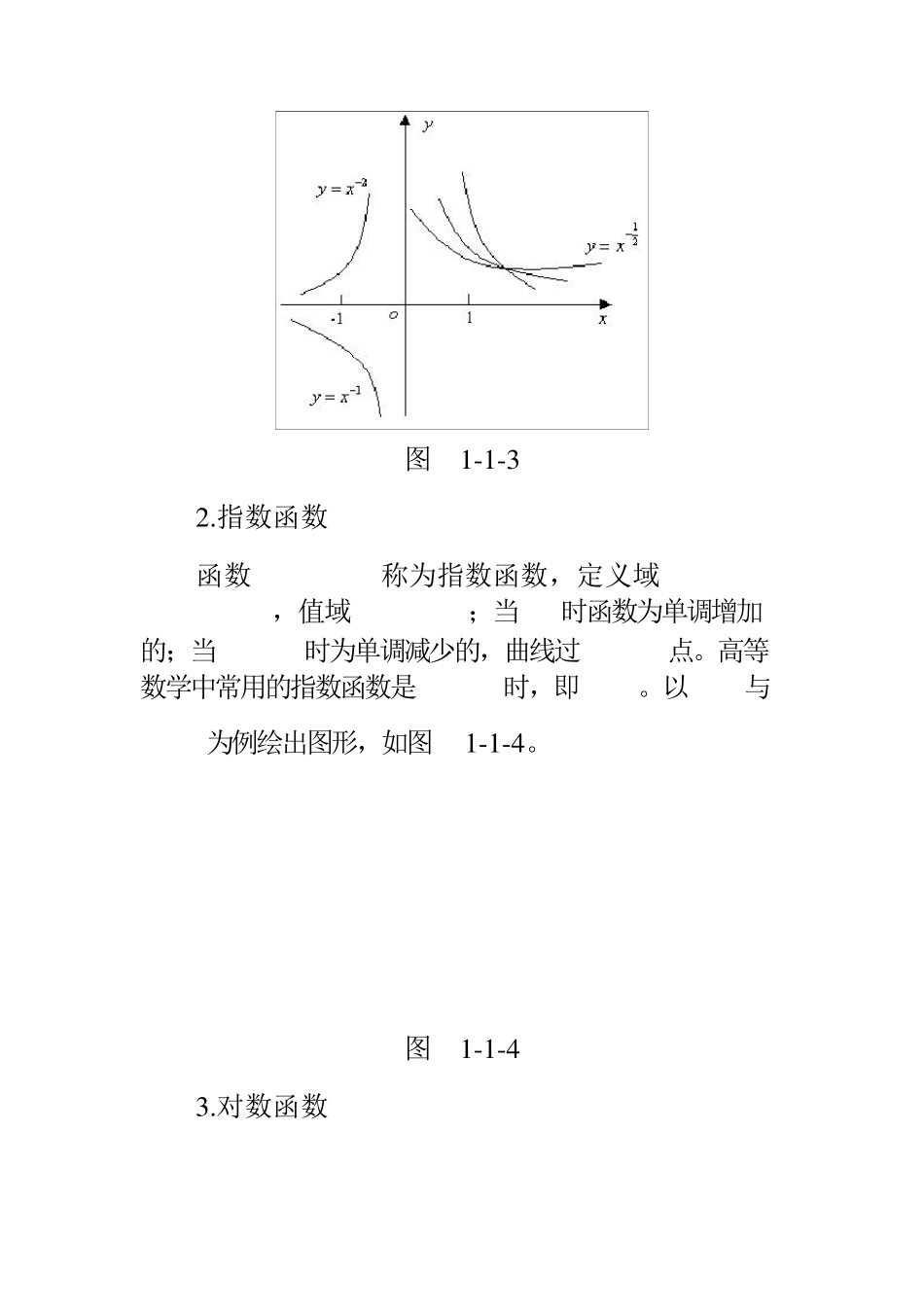
五、基本初等函数及其性质和图形 1 .幂函数 函数称为幂函数。如,,,都是幂函数。没有统一的定义域,定义域由 值确定。如,。但在内总是有定义的,且都经过(1 ,1 )点。当 时,函数在上是单调增加的,当时,函数在内是单调减少的。下面给出几个常用的幂函数:的图形,如图 1 -1 -2 、图1 -1 -3 。 图 1 -1 -2 图 1 -1 -3 2 .指数函数 函数称为指数函数,定义域,值域;当时函数为单调增加的;当 时为单调减少的,曲线过 点。高等数学中常用的指数函数是 时,即。以与为例绘出图形,如图1 -1 -4 。 图 1 -1 -4 3 .对数函数 函数 称为对数函数,其定义域 ,值域。当时单调增加,当时单调减少,曲线过(1 ,0 )点,都在右半平面内。 与互为反函数。当时的对数函数称为自然对数,当时,称为常用对数。以为例绘出图形,如图1 -1 -5 。 图 1 -1 -5 4 .三角函数 有,它们都是周期函数。对三角函数作简要的叙述: (1)正弦函数与余弦函数:与定义域都是,值域都是。它们都是有界函数,周期都是,为奇函数,为偶函数。图形为图1 -1 -6 、图1 -1 -7 。 图 1 -1 -6 正弦函数图形 图 1 -1 -7 余弦函数图形 (2)正切函数,定义域,值域为。周期,在其定义域内单调增加的奇函数,图形为图1 -1 -8 图 1 -1 -8 (3)余切函数,定义域,值域为,周期。在定义域内是单调减少的奇函数,图形如图1-1-9 。 图 1 -1 -9 (4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1 -1 -1 0 。 图 1 -1 -1 0 (5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11 。 图 1 -1 -1 1 5 .反三角函数 反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1 -1 -1 2 ; 图 1 -1 -1 2 反余弦函数 ,定义域为[-1,1],值域为 ,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图 1-1-13; 图 1-1-13 反正切函数 ,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图 1-1-14; 图 1-1-14 反余切函数 ,定义域为,值域,为有界函数,在其定义域内单调减少的非奇非偶函数。图形如图 1 -1 -1 5 。 图 1 -1 -1 5