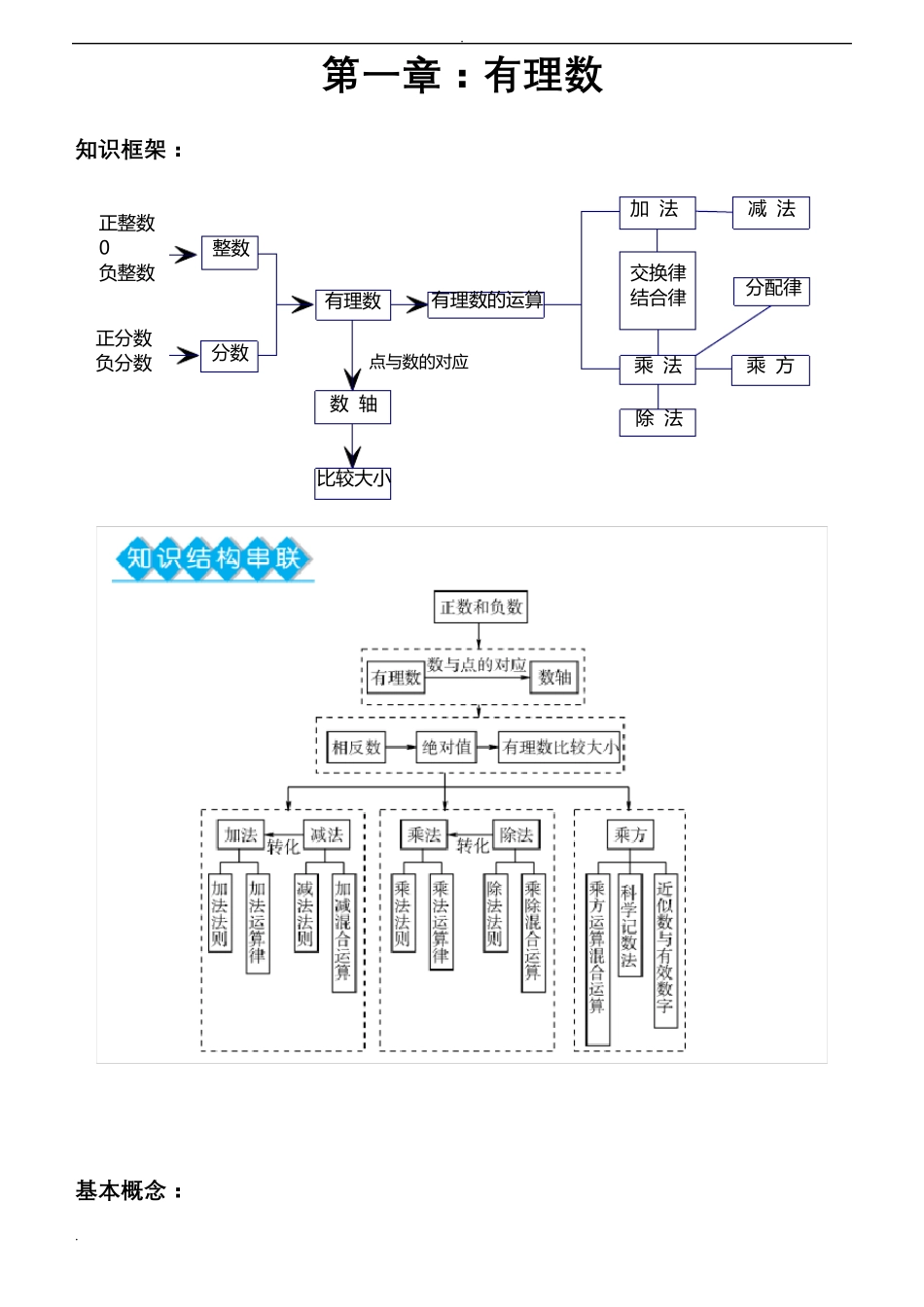
. . 第 一 章 : 有 理 数 知 识 框 架 : 基 本 概 念 : 有 理 数 的 运 算分 配 律除 法乘 方乘 法交 换 律结 合 律减 法 加 法比 较 大 小数 轴点 与数 的 对应有 理 数分 数整数正分 数负分 数 正整数0负整数. . 1.大于 0 的数叫做正 数 。 2.在正数前面加上负号“-”的数叫做负 数 。 3.整 数和 分 数统 称 为 有 理 数 。 4.人 们 通 常 用 一 条 直 线 上的点 表 示 数, 这 条 直 线 叫做数 轴 。 5.在直 线 上任 取 一 个 点 表 示 数 0, 这 个 点 叫做原 点 。 6.一 般 的, 数轴 上表 示 数 a 的点 与 原 点 的距 离 叫做数 a 的绝 对 值 。 7.由 绝 对 值 的定 义 可 知 : ( 1) 一 个 正 数 的 绝 对 值 是 它 本 身 ; 一 个 负 数 的 绝 对 值 是 它 的 相 反 数 ; 0 的 绝 对 值 是 0。 ( 2) 正 数 大 于 0, 0 大 于 负 数 , 正 数 大 于 负 数 。 ( 3) 两 个 负 数 , 绝 对 值 大 的 反 而 小 。 8.有 理 数加法 法 则 : ( 1) 同 号 两 数 相 加 , 取 相 同 的 符 号 , 并 把 绝 对 值 相 加 。 ( 2) 绝 对 值 不 相 等 的 异 号 两 数 相 加 , 取 绝 对 值 较 大 的 加 数 的 负 号 , 并 用 较 大 的 绝 对 值 减 去 较 小 的 绝 对 值 , 互为 相 反 数 的 两 个 数 相 加 得 0。 ( 3) 一 个 数 同 0 相 加 , 仍 得 这 个 数 。 9.有 理 数的加法 中 , 两 个 数 相 加 , 交 换 交 换 加 数 的 位 置 , 和 不 变 。 10.有 理 数的加法 中 , 三 个 数 相 加 , 先 把 前 两 个 数 相 加 , 或 者 先 把 后 两 个 数 相 加 , 和 不 变 。 11.有 理 数减 法 法 则 减 去 一 个 数 , 等 于 加 上 这 个 数 的 相 反 数 。 12.有 理 数乘 法 法 则 两 数 相 乘 , 同 号 得 正 , 异 号 得 负 , 并 把 绝 对 值 向 乘 。 任 何 数 同 0 相 乘 , 都 得 0。 13.有 理 数中 仍 然 有 : 乘 积 是 1 的 两 个 数 互 为...