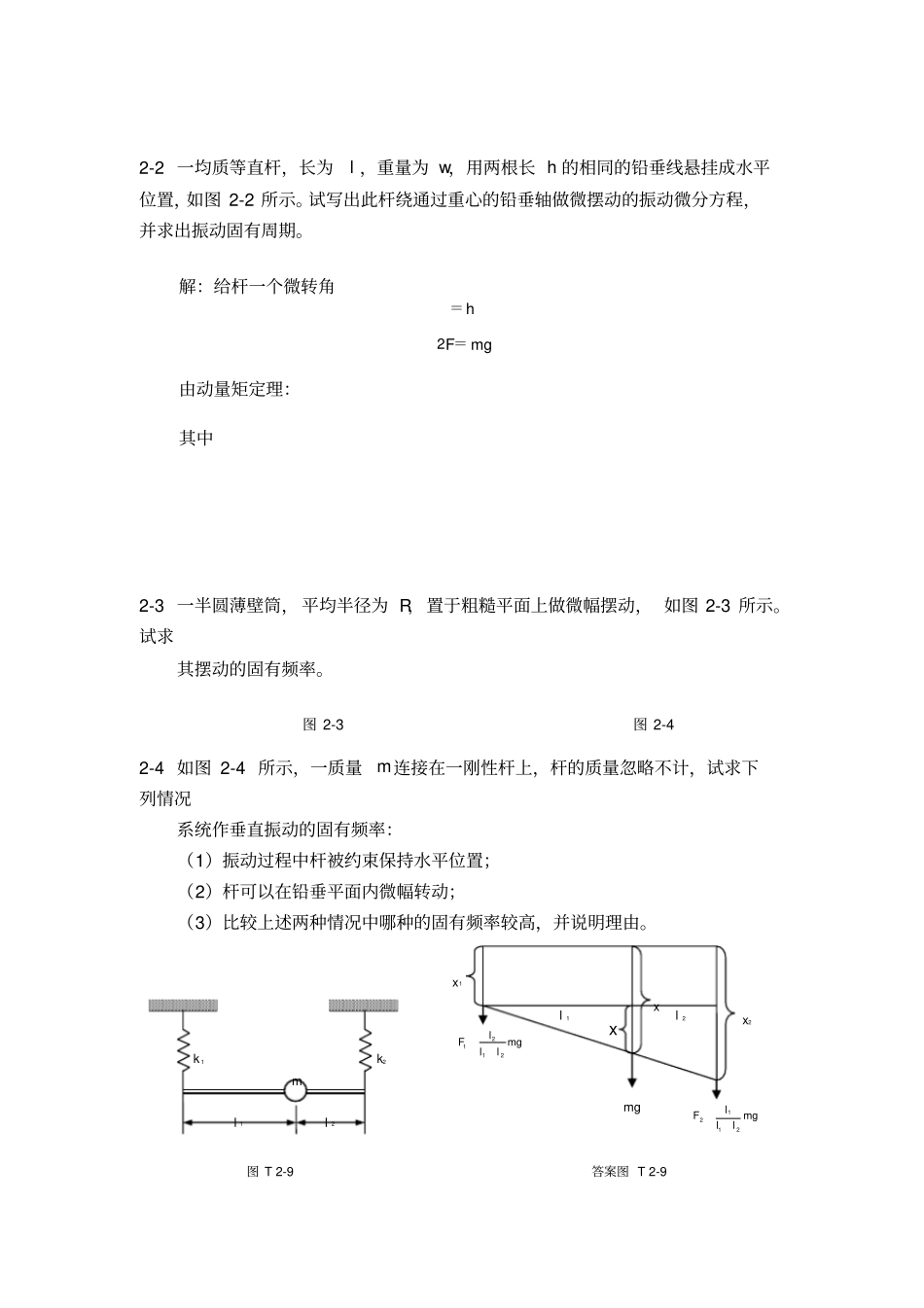
第二章 单自由度系统的自由振动2-1 如图 2-1 所示,重物1W 悬挂在刚度为 k 的弹簧上并处于静止平衡位置,另一重物2W 从高度为 h 处自由下落到1W 上且无弹跳。试求2W 下降的最大距离和两物体碰撞后的运动规律。解:222221vgWhW,ghv22动量守恒:122122vgWWvgW,ghWWWv221212平衡位置:11kxW,kWx111221kxWW,kWWx2112故:kWxxx211202121WWkggWWkn故:tvtxtxtxxnnnnnnsincossincos12000xxx 1x12平衡位置2-2 一均质等直杆,长为l ,重量为 w,用两根长 h 的相同的铅垂线悬挂成水平位置,如图 2-2 所示。试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程,并求出振动固有周期。解:给杆一个微转角=h2F= mg由动量矩定理:其中2-3 一半圆薄壁筒, 平均半径为 R, 置于粗糙平面上做微幅摆动, 如图 2-3 所示。试求其摆动的固有频率。图 2-3 图 2-42-4 如图 2-4 所示,一质量m连接在一刚性杆上,杆的质量忽略不计,试求下列情况系统作垂直振动的固有频率:(1)振动过程中杆被约束保持水平位置;(2)杆可以在铅垂平面内微幅转动;(3)比较上述两种情况中哪种的固有频率较高,并说明理由。图 T 2-9 答案图 T 2-9mglllF2112mgl 1l 2x1x2xxmglllF2121k2k 1ml 1l 2解:(1)保持水平位置:mkkn21(2)微幅转动:mgkkllklklmgkkllkllklllklmgkkllklkllllkllmglmgklllkllllllkllmgllllxxkFxxx2122122212121221221121212221212211211121212122211211121221112111故:22212121221klklkkllkemken2-5 试求图 2-5 所示系统中均质刚性杆AB在 A 点的等效质量。已知杆的质量为m,A端弹簧的刚度为 k。并问铰链支座C放在何处时使系统的固有频率最高?图 2-5 图 2-62-6 在图 2-6 所示的系统中,四个弹簧均未受力。已知m=50kg,19800 N mk,234900 N mkk,419600 N mk。试问:(1)若将支撑缓慢撤去,质量块将下落多少距离?(2)若将支撑突然撤去,质量块又将下落多少距离?{} 图 T 2-17 所示的系统中,四个弹簧均未受力,k1= k 2= k 3= k 4= k ,试问:(1)若将支承缓慢撤去,质量块将下落多少距离?(2)若将支承突然撤去,质量块又将下落多少距离?图 T 2-17解:kkkkkkkkkkkkkkkk213224123412312342312311233223(1)01234 xkmg,kmgx20(2)txtxncos0,kmgxx420max2-7 图 2-7 所示系统,质量为m2的均质圆盘在水平面上作无滑动的滚动,鼓轮绕轴的转动惯量为I ,忽略绳子的弹...